12345qiupeng
/
gtsam
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

Merge branch 'develop' into jeffrey/isam2_marginalization

release/4.3a0
Varun Agrawal 2024-12-06 16:57:02 -05:00
parent 06dac43cae 628111202d
commit 5f832fc6dd
79 changed files with 3694 additions and 1048 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

6
.github/workflows/build-macos.yml vendored
View File

@ -25,15 +25,15 @@ jobs:
# Github Actions requires a single row to be added to the build matrix.
# See https://help.github.com/en/articles/workflow-syntax-for-github-actions.
name: [
macos-12-xcode-14.2,
macos-13-xcode-14.2,
macos-14-xcode-15.4,
]
build_type: [Debug, Release]
build_unstable: [ON]
include:
- name: macos-12-xcode-14.2
os: macos-12
- name: macos-13-xcode-14.2
os: macos-13
compiler: xcode
version: "14.2"

6
.github/workflows/build-python.yml vendored
View File

@ -30,7 +30,7 @@ jobs:
[
ubuntu-20.04-gcc-9,
ubuntu-20.04-clang-9,
macos-12-xcode-14.2,
macos-13-xcode-14.2,
macos-14-xcode-15.4,
windows-2022-msbuild,
]
@ -48,8 +48,8 @@ jobs:
compiler: clang
version: "9"
- name: macos-12-xcode-14.2
os: macos-12
- name: macos-13-xcode-14.2
os: macos-13
compiler: xcode
version: "14.2"

8
CMakeLists.txt
View File

@ -1,4 +1,4 @@
cmake_minimum_required(VERSION 3.5)
cmake_minimum_required(VERSION 3.9)
if (POLICY CMP0082)
cmake_policy(SET CMP0082 NEW) # install from sub-directories immediately
endif()
@ -12,6 +12,12 @@ if (POLICY CMP0167)
cmake_policy(SET CMP0167 OLD) # Don't complain about boost
endif()
# allow parent project to override options
if (POLICY CMP0077)
cmake_policy(SET CMP0077 NEW)
endif(POLICY CMP0077)
# Set the version number for the library
set (GTSAM_VERSION_MAJOR 4)
set (GTSAM_VERSION_MINOR 3)

56
cmake/FindGooglePerfTools.cmake
View File

@ -1,42 +1,40 @@
# -*- cmake -*-
# - Find Google perftools
# Find the Google perftools includes and libraries
# This module defines
# GOOGLE_PERFTOOLS_INCLUDE_DIR, where to find heap-profiler.h, etc.
# GOOGLE_PERFTOOLS_FOUND, If false, do not try to use Google perftools.
# also defined for general use are
# TCMALLOC_LIBRARY, where to find the tcmalloc library.
FIND_PATH(GOOGLE_PERFTOOLS_INCLUDE_DIR google/heap-profiler.h
/usr/local/include
/usr/include
)
# - Find GPerfTools (formerly Google perftools)
# Find the GPerfTools libraries
# If false, do not try to use Google perftools.
# Also defined for general use are
# - GPERFTOOLS_TCMALLOC: where to find the tcmalloc library
# - GPERFTOOLS_PROFILER: where to find the profiler library
SET(TCMALLOC_NAMES ${TCMALLOC_NAMES} tcmalloc)
FIND_LIBRARY(TCMALLOC_LIBRARY
find_library(GPERFTOOLS_TCMALLOC
NAMES ${TCMALLOC_NAMES}
PATHS /usr/lib /usr/local/lib
)
)
find_library(GPERFTOOLS_PROFILER
NAMES profiler
PATHS /usr/lib /usr/local/lib
)
IF (TCMALLOC_LIBRARY AND GOOGLE_PERFTOOLS_INCLUDE_DIR)
SET(TCMALLOC_LIBRARIES ${TCMALLOC_LIBRARY})
SET(GOOGLE_PERFTOOLS_FOUND "YES")
ELSE (TCMALLOC_LIBRARY AND GOOGLE_PERFTOOLS_INCLUDE_DIR)
SET(GOOGLE_PERFTOOLS_FOUND "NO")
ENDIF (TCMALLOC_LIBRARY AND GOOGLE_PERFTOOLS_INCLUDE_DIR)
IF (GPERFTOOLS_TCMALLOC AND GPERFTOOLS_PROFILER)
SET(TCMALLOC_LIBRARIES ${GPERFTOOLS_TCMALLOC})
SET(GPERFTOOLS_FOUND "YES")
ELSE (GPERFTOOLS_TCMALLOC AND GPERFTOOLS_PROFILER)
SET(GPERFTOOLS_FOUND "NO")
ENDIF (GPERFTOOLS_TCMALLOC AND GPERFTOOLS_PROFILER)
IF (GOOGLE_PERFTOOLS_FOUND)
IF (NOT GOOGLE_PERFTOOLS_FIND_QUIETLY)
MESSAGE(STATUS "Found Google perftools: ${GOOGLE_PERFTOOLS_LIBRARIES}")
ENDIF (NOT GOOGLE_PERFTOOLS_FIND_QUIETLY)
ELSE (GOOGLE_PERFTOOLS_FOUND)
IF (GPERFTOOLS_FOUND)
MESSAGE(STATUS "Found Gperftools: ${GPERFTOOLS_PROFILER}")
ELSE (GPERFTOOLS_FOUND)
IF (GOOGLE_PERFTOOLS_FIND_REQUIRED)
MESSAGE(FATAL_ERROR "Could not find Google perftools library")
ENDIF (GOOGLE_PERFTOOLS_FIND_REQUIRED)
ENDIF (GOOGLE_PERFTOOLS_FOUND)
ENDIF (GPERFTOOLS_FOUND)
MARK_AS_ADVANCED(
TCMALLOC_LIBRARY
GOOGLE_PERFTOOLS_INCLUDE_DIR
)
GPERFTOOLS_TCMALLOC
GPERFTOOLS_PROFILER
)
option(GTSAM_ENABLE_GPERFTOOLS "Enable/Disable Gperftools" OFF)

2
cmake/HandleAllocators.cmake
View File

@ -7,7 +7,7 @@ else()
list(APPEND possible_allocators BoostPool STL)
set(preferred_allocator STL)
endif()
if(GOOGLE_PERFTOOLS_FOUND)
if(GPERFTOOLS_FOUND)
list(APPEND possible_allocators tcmalloc)
endif()

2
cmake/HandlePerfTools.cmake
View File

@ -1,4 +1,4 @@
###############################################################################
# Find Google perftools
find_package(GooglePerfTools)
find_package(GooglePerfTools)

138
examples/EssentialViewGraphExample.cpp Normal file
View File

@ -0,0 +1,138 @@
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010, Georgia Tech Research Corporation,
* Atlanta, Georgia 30332-0415
* All Rights Reserved
* Authors: Frank Dellaert, et al. (see THANKS for the full author list)
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/**
* @file EssentialViewGraphExample.cpp
* @brief View-graph calibration with essential matrices.
* @author Frank Dellaert
* @date October 2024
*/
#include <gtsam/geometry/Cal3f.h>
#include <gtsam/geometry/EssentialMatrix.h>
#include <gtsam/geometry/PinholeCamera.h>
#include <gtsam/geometry/Point2.h>
#include <gtsam/geometry/Point3.h>
#include <gtsam/geometry/Pose3.h>
#include <gtsam/inference/EdgeKey.h>
#include <gtsam/inference/Symbol.h>
#include <gtsam/nonlinear/LevenbergMarquardtOptimizer.h>
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
#include <gtsam/nonlinear/Values.h>
#include <gtsam/sfm/TransferFactor.h> // Contains EssentialTransferFactorK
#include <vector>
#include "SFMdata.h" // For createPoints() and posesOnCircle()
using namespace std;
using namespace gtsam;
using namespace symbol_shorthand; // For K(symbol)
// Main function
int main(int argc, char* argv[]) {
// Define the camera calibration parameters
Cal3f cal(50.0, 50.0, 50.0);
// Create the set of 8 ground-truth landmarks
vector<Point3> points = createPoints();
// Create the set of 4 ground-truth poses
vector<Pose3> poses = posesOnCircle(4, 30);
// Calculate ground truth essential matrices, 1 and 2 poses apart
auto E1 = EssentialMatrix::FromPose3(poses[0].between(poses[1]));
auto E2 = EssentialMatrix::FromPose3(poses[0].between(poses[2]));
// Simulate measurements from each camera pose
std::array<std::array<Point2, 8>, 4> p;
for (size_t i = 0; i < 4; ++i) {
PinholeCamera<Cal3f> camera(poses[i], cal);
for (size_t j = 0; j < 8; ++j) {
p[i][j] = camera.project(points[j]);
}
}
// Create the factor graph
NonlinearFactorGraph graph;
using Factor = EssentialTransferFactorK<Cal3f>;
for (size_t a = 0; a < 4; ++a) {
size_t b = (a + 1) % 4; // Next camera
size_t c = (a + 2) % 4; // Camera after next
// Vectors to collect tuples for each factor
std::vector<std::tuple<Point2, Point2, Point2>> tuples1, tuples2, tuples3;
// Collect data for the three factors
for (size_t j = 0; j < 8; ++j) {
tuples1.emplace_back(p[a][j], p[b][j], p[c][j]);
tuples2.emplace_back(p[a][j], p[c][j], p[b][j]);
tuples3.emplace_back(p[c][j], p[b][j], p[a][j]);
}
// Add transfer factors between views a, b, and c.
graph.emplace_shared<Factor>(EdgeKey(a, c), EdgeKey(b, c), tuples1);
graph.emplace_shared<Factor>(EdgeKey(a, b), EdgeKey(b, c), tuples2);
graph.emplace_shared<Factor>(EdgeKey(a, c), EdgeKey(a, b), tuples3);
}
// Formatter for printing keys
auto formatter = [](Key key) {
if (Symbol(key).chr() == 'k') {
return (string)Symbol(key);
} else {
EdgeKey edge(key);
return (std::string)edge;
}
};
graph.print("Factor Graph:\n", formatter);
// Create a delta vector to perturb the ground truth (small perturbation)
Vector5 delta;
delta << 1, 1, 1, 1, 1;
delta *= 1e-2;
// Create the initial estimate for essential matrices
Values initialEstimate;
for (size_t a = 0; a < 4; ++a) {
size_t b = (a + 1) % 4; // Next camera
size_t c = (a + 2) % 4; // Camera after next
initialEstimate.insert(EdgeKey(a, b), E1.retract(delta));
initialEstimate.insert(EdgeKey(a, c), E2.retract(delta));
}
// Insert initial calibrations (using K symbol)
for (size_t i = 0; i < 4; ++i) {
initialEstimate.insert(K(i), cal);
}
initialEstimate.print("Initial Estimates:\n", formatter);
graph.printErrors(initialEstimate, "Initial Errors:\n", formatter);
// Optimize the graph and print results
LevenbergMarquardtParams params;
params.setlambdaInitial(1000.0); // Initialize lambda to a high value
params.setVerbosityLM("SUMMARY");
Values result =
LevenbergMarquardtOptimizer(graph, initialEstimate, params).optimize();
cout << "Initial error = " << graph.error(initialEstimate) << endl;
cout << "Final error = " << graph.error(result) << endl;
result.print("Final Results:\n", formatter);
E1.print("Ground Truth E1:\n");
E2.print("Ground Truth E2:\n");
return 0;
}

2
examples/SFMdata.h
View File

@ -56,7 +56,7 @@ std::vector<Point3> createPoints() {
/**
* Create a set of ground-truth poses
* Default values give a circular trajectory, radius 30 at pi/4 intervals,
* Default values give a circular trajectory, radius 30 at pi/4 intervals,
* always facing the circle center
*/
std::vector<Pose3> createPoses(

10
examples/ViewGraphExample.cpp
View File

@ -38,7 +38,7 @@ using namespace gtsam;
/* ************************************************************************* */
int main(int argc, char* argv[]) {
// Define the camera calibration parameters
Cal3_S2 K(50.0, 50.0, 0.0, 50.0, 50.0);
Cal3_S2 cal(50.0, 50.0, 0.0, 50.0, 50.0);
// Create the set of 8 ground-truth landmarks
vector<Point3> points = createPoints();
@ -47,13 +47,13 @@ int main(int argc, char* argv[]) {
vector<Pose3> poses = posesOnCircle(4, 30);
// Calculate ground truth fundamental matrices, 1 and 2 poses apart
auto F1 = FundamentalMatrix(K, poses[0].between(poses[1]), K);
auto F2 = FundamentalMatrix(K, poses[0].between(poses[2]), K);
auto F1 = FundamentalMatrix(cal.K(), poses[0].between(poses[1]), cal.K());
auto F2 = FundamentalMatrix(cal.K(), poses[0].between(poses[2]), cal.K());
// Simulate measurements from each camera pose
std::array<std::array<Point2, 8>, 4> p;
for (size_t i = 0; i < 4; ++i) {
PinholeCamera<Cal3_S2> camera(poses[i], K);
PinholeCamera<Cal3_S2> camera(poses[i], cal);
for (size_t j = 0; j < 8; ++j) {
p[i][j] = camera.project(points[j]);
}
@ -114,7 +114,7 @@ int main(int argc, char* argv[]) {
initialEstimate.insert(EdgeKey(a, c), F2.retract(delta));
}
initialEstimate.print("Initial Estimates:\n", formatter);
graph.printErrors(initialEstimate, "errors: ", formatter);
graph.printErrors(initialEstimate, "errors: ", formatter);
/* Optimize the graph and print results */
LevenbergMarquardtParams params;

4
gtsam/CMakeLists.txt
View File

@ -147,6 +147,10 @@ if (GTSAM_USE_EIGEN_MKL)
target_include_directories(gtsam PUBLIC ${MKL_INCLUDE_DIR})
endif()
if (GTSAM_ENABLE_GPERFTOOLS AND GPERFTOOLS_FOUND)
target_link_libraries(gtsam PRIVATE ${GPERFTOOLS_TCMALLOC} ${GPERFTOOLS_PROFILER})
endif()
# Add includes for source directories 'BEFORE' boost and any system include
# paths so that the compiler uses GTSAM headers in our source directory instead
# of any previously installed GTSAM headers.

3
gtsam/base/Vector.h
View File

@ -16,6 +16,7 @@
* @author Frank Dellaert
* @author Alex Hagiopol
* @author Varun Agrawal
* @author Fan Jiang
*/
// \callgraph
@ -193,14 +194,12 @@ GTSAM_EXPORT Vector ediv_(const Vector &a, const Vector &b);
*/
template<class V1, class V2>
inline double dot(const V1 &a, const V2& b) {
assert (b.size()==a.size());
return a.dot(b);
}
/** compatibility version for ublas' inner_prod() */
template<class V1, class V2>
inline double inner_prod(const V1 &a, const V2& b) {
assert (b.size()==a.size());
return a.dot(b);
}

126
gtsam/discrete/DecisionTreeFactor.cpp
View File

@ -239,7 +239,7 @@ namespace gtsam {
};
// Go through the tree
this->apply(op);
this->visitWith(op);
return probs;
}
@ -349,22 +349,122 @@ namespace gtsam {
: DiscreteFactor(keys.indices(), keys.cardinalities()),
AlgebraicDecisionTree<Key>(keys, table) {}
/**
* @brief Min-Heap class to help with pruning.
* The `top` element is always the smallest value.
*/
class MinHeap {
std::vector<double> v_;
public:
/// Default constructor
MinHeap() {}
/// Push value onto the heap
void push(double x) {
v_.push_back(x);
std::push_heap(v_.begin(), v_.end(), std::greater<double>{});
}
/// Push value `x`, `n` number of times.
void push(double x, size_t n) {
for (size_t i = 0; i < n; ++i) {
v_.push_back(x);
std::push_heap(v_.begin(), v_.end(), std::greater<double>{});
}
}
/// Pop the top value of the heap.
double pop() {
std::pop_heap(v_.begin(), v_.end(), std::greater<double>{});
double x = v_.back();
v_.pop_back();
return x;
}
/// Return the top value of the heap without popping it.
double top() { return v_.at(0); }
/**
* @brief Print the heap as a sequence.
*
* @param s A string to prologue the output.
*/
void print(const std::string& s = "") {
std::cout << (s.empty() ? "" : s + " ");
for (size_t i = 0; i < v_.size(); i++) {
std::cout << v_.at(i);
if (v_.size() > 1 && i < v_.size() - 1) std::cout << ", ";
}
std::cout << std::endl;
}
/// Return true if heap is empty.
bool empty() const { return v_.empty(); }
/// Return the size of the heap.
size_t size() const { return v_.size(); }
};
/* ************************************************************************ */
double DecisionTreeFactor::computeThreshold(const size_t N) const {
// Set of all keys
std::set<Key> allKeys = this->labels();
MinHeap min_heap;
auto op = [&](const Assignment<Key>& a, double p) {
// Get all the keys in the current assignment
std::set<Key> assignment_keys;
for (auto&& [k, _] : a) {
assignment_keys.insert(k);
}
// Find the keys missing in the assignment
std::vector<Key> diff;
std::set_difference(allKeys.begin(), allKeys.end(),
assignment_keys.begin(), assignment_keys.end(),
std::back_inserter(diff));
// Compute the total number of assignments in the (pruned) subtree
size_t nrAssignments = 1;
for (auto&& k : diff) {
nrAssignments *= cardinalities_.at(k);
}
// If min-heap is empty, fill it initially.
// This is because there is nothing at the top.
if (min_heap.empty()) {
min_heap.push(p, std::min(nrAssignments, N));
} else {
for (size_t i = 0; i < std::min(nrAssignments, N); ++i) {
// If p is larger than the smallest element,
// then we insert into the min heap.
// We check against the top each time because the
// heap maintains the smallest element at the top.
if (p > min_heap.top()) {
if (min_heap.size() == N) {
min_heap.pop();
}
min_heap.push(p);
} else {
// p is <= min value so move to the next one
break;
}
}
}
return p;
};
this->visitWith(op);
return min_heap.top();
}
/* ************************************************************************ */
DecisionTreeFactor DecisionTreeFactor::prune(size_t maxNrAssignments) const {
const size_t N = maxNrAssignments;
// Get the probabilities in the decision tree so we can threshold.
std::vector<double> probabilities = this->probabilities();
// The number of probabilities can be lower than max_leaves
if (probabilities.size() <= N) {
return *this;
}
std::sort(probabilities.begin(), probabilities.end(),
std::greater<double>{});
double threshold = probabilities[N - 1];
double threshold = computeThreshold(N);
// Now threshold the decision tree
size_t total = 0;

11
gtsam/discrete/DecisionTreeFactor.h
View File

@ -224,6 +224,17 @@ namespace gtsam {
/// Get all the probabilities in order of assignment values
std::vector<double> probabilities() const;
/**
* @brief Compute the probability value which is the threshold above which
* only `N` leaves are present.
*
* This is used for pruning out the smaller probabilities.
*
* @param N The number of leaves to keep post pruning.
* @return double
*/
double computeThreshold(const size_t N) const;
/**
* @brief Prune the decision tree of discrete variables.
*

45
gtsam/discrete/tests/testDecisionTreeFactor.cpp
View File

@ -140,11 +140,46 @@ TEST(DecisionTreeFactor, enumerate) {
EXPECT(actual == expected);
}
namespace pruning_fixture {
DiscreteKey A(1, 2), B(2, 2), C(3, 2);
DecisionTreeFactor f(A& B& C, "1 5 3 7 2 6 4 8");
DiscreteKey D(4, 2);
DecisionTreeFactor factor(
D& C & B & A,
"0.0 0.0 0.0 0.60658897 0.61241912 0.61241969 0.61247685 0.61247742 0.0 "
"0.0 0.0 0.99995287 1.0 1.0 1.0 1.0");
} // namespace pruning_fixture
/* ************************************************************************* */
// Check if computing the correct threshold works.
TEST(DecisionTreeFactor, ComputeThreshold) {
using namespace pruning_fixture;
// Only keep the leaves with the top 5 values.
double threshold = f.computeThreshold(5);
EXPECT_DOUBLES_EQUAL(4.0, threshold, 1e-9);
// Check for more extreme pruning where we only keep the top 2 leaves
threshold = f.computeThreshold(2);
EXPECT_DOUBLES_EQUAL(7.0, threshold, 1e-9);
threshold = factor.computeThreshold(5);
EXPECT_DOUBLES_EQUAL(0.99995287, threshold, 1e-9);
threshold = factor.computeThreshold(3);
EXPECT_DOUBLES_EQUAL(1.0, threshold, 1e-9);
threshold = factor.computeThreshold(6);
EXPECT_DOUBLES_EQUAL(0.61247742, threshold, 1e-9);
}
/* ************************************************************************* */
// Check pruning of the decision tree works as expected.
TEST(DecisionTreeFactor, Prune) {
DiscreteKey A(1, 2), B(2, 2), C(3, 2);
DecisionTreeFactor f(A & B & C, "1 5 3 7 2 6 4 8");
using namespace pruning_fixture;
// Only keep the leaves with the top 5 values.
size_t maxNrAssignments = 5;
@ -160,12 +195,6 @@ TEST(DecisionTreeFactor, Prune) {
DecisionTreeFactor expected2(A & B & C, "0 0 0 7 0 0 0 8");
EXPECT(assert_equal(expected2, pruned2));
DiscreteKey D(4, 2);
DecisionTreeFactor factor(
D & C & B & A,
"0.0 0.0 0.0 0.60658897 0.61241912 0.61241969 0.61247685 0.61247742 0.0 "
"0.0 0.0 0.99995287 1.0 1.0 1.0 1.0");
DecisionTreeFactor expected3(D & C & B & A,
"0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 "
"0.999952870000 1.0 1.0 1.0 1.0");

6
gtsam/geometry/Cal3Bundler.cpp
View File

@ -56,10 +56,8 @@ void Cal3Bundler::print(const std::string& s) const {
/* ************************************************************************* */
bool Cal3Bundler::equals(const Cal3Bundler& K, double tol) const {
const Cal3* base = dynamic_cast<const Cal3*>(&K);
return (Cal3::equals(*base, tol) && std::fabs(k1_ - K.k1_) < tol &&
std::fabs(k2_ - K.k2_) < tol && std::fabs(u0_ - K.u0_) < tol &&
std::fabs(v0_ - K.v0_) < tol);
return Cal3f::equals(static_cast<const Cal3f&>(K), tol) &&
std::fabs(k1_ - K.k1_) < tol && std::fabs(k2_ - K.k2_) < tol;
}
/* ************************************************************************* */

41
gtsam/geometry/Cal3Bundler.h
View File

@ -19,7 +19,7 @@
#pragma once
#include <gtsam/geometry/Cal3.h>
#include <gtsam/geometry/Cal3f.h>
#include <gtsam/geometry/Point2.h>
namespace gtsam {
@ -29,22 +29,18 @@ namespace gtsam {
* @ingroup geometry
* \nosubgrouping
*/
class GTSAM_EXPORT Cal3Bundler : public Cal3 {
class GTSAM_EXPORT Cal3Bundler : public Cal3f {
private:
double k1_ = 0.0f, k2_ = 0.0f; ///< radial distortion
double tol_ = 1e-5; ///< tolerance value when calibrating
double k1_ = 0.0, k2_ = 0.0; ///< radial distortion coefficients
double tol_ = 1e-5; ///< tolerance value when calibrating
// NOTE: We use the base class fx to represent the common focal length.
// Also, image center parameters (u0, v0) are not optimized
// but are treated as constants.
// Note: u0 and v0 are constants and not optimized.
public:
enum { dimension = 3 };
///< shared pointer to stereo calibration object
using shared_ptr = std::shared_ptr<Cal3Bundler>;
/// @name Standard Constructors
/// @name Constructors
/// @{
/// Default constructor
@ -61,9 +57,9 @@ class GTSAM_EXPORT Cal3Bundler : public Cal3 {
*/
Cal3Bundler(double f, double k1, double k2, double u0 = 0, double v0 = 0,
double tol = 1e-5)
: Cal3(f, f, 0, u0, v0), k1_(k1), k2_(k2), tol_(tol) {}
: Cal3f(f, u0, v0), k1_(k1), k2_(k2), tol_(tol) {}
~Cal3Bundler() override {}
~Cal3Bundler() override = default;
/// @}
/// @name Testable
@ -77,24 +73,18 @@ class GTSAM_EXPORT Cal3Bundler : public Cal3 {
void print(const std::string& s = "") const override;
/// assert equality up to a tolerance
bool equals(const Cal3Bundler& K, double tol = 10e-9) const;
bool equals(const Cal3Bundler& K, double tol = 1e-9) const;
/// @}
/// @name Standard Interface
/// @{
/// distorsion parameter k1
/// distortion parameter k1
inline double k1() const { return k1_; }
/// distorsion parameter k2
/// distortion parameter k2
inline double k2() const { return k2_; }
/// image center in x
inline double px() const { return u0_; }
/// image center in y
inline double py() const { return v0_; }
Matrix3 K() const override; ///< Standard 3*3 calibration matrix
Vector4 k() const; ///< Radial distortion parameters (4 of them, 2 0)
@ -113,8 +103,7 @@ class GTSAM_EXPORT Cal3Bundler : public Cal3 {
/**
* Convert a pixel coordinate to ideal coordinate xy
* @param p point in image coordinates
* @param tol optional tolerance threshold value for iterative minimization
* @param pi point in image coordinates
* @param Dcal optional 2*3 Jacobian wrpt Cal3Bundler parameters
* @param Dp optional 2*2 Jacobian wrpt intrinsic coordinates
* @return point in intrinsic coordinates
@ -135,14 +124,14 @@ class GTSAM_EXPORT Cal3Bundler : public Cal3 {
/// @name Manifold
/// @{
/// return DOF, dimensionality of tangent space
/// Return DOF, dimensionality of tangent space
size_t dim() const override { return Dim(); }
/// return DOF, dimensionality of tangent space
/// Return DOF, dimensionality of tangent space
inline static size_t Dim() { return dimension; }
/// Update calibration with tangent space delta
inline Cal3Bundler retract(const Vector& d) const {
Cal3Bundler retract(const Vector& d) const {
return Cal3Bundler(fx_ + d(0), k1_ + d(1), k2_ + d(2), u0_, v0_);
}

106
gtsam/geometry/Cal3f.cpp Normal file
View File

@ -0,0 +1,106 @@
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010, Georgia Tech Research Corporation,
* Atlanta, Georgia 30332-0415
* All Rights Reserved
* Authors: Frank Dellaert, et al. (see THANKS for the full author list)
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/**
* @file Cal3f.cpp
* @brief Implementation file for Cal3f class
* @author Frank Dellaert
* @date October 2024
*/
#include <gtsam/base/Matrix.h>
#include <gtsam/base/Vector.h>
#include <gtsam/geometry/Cal3f.h>
#include <iostream>
namespace gtsam {
/* ************************************************************************* */
Cal3f::Cal3f(double f, double u0, double v0) : Cal3(f, f, 0.0, u0, v0) {}
/* ************************************************************************* */
std::ostream& operator<<(std::ostream& os, const Cal3f& cal) {
os << "f: " << cal.fx_ << ", px: " << cal.u0_ << ", py: " << cal.v0_;
return os;
}
/* ************************************************************************* */
void Cal3f::print(const std::string& s) const {
if (!s.empty()) std::cout << s << " ";
std::cout << *this << std::endl;
}
/* ************************************************************************* */
bool Cal3f::equals(const Cal3f& K, double tol) const {
return Cal3::equals(static_cast<const Cal3&>(K), tol);
}
/* ************************************************************************* */
Vector1 Cal3f::vector() const {
Vector1 v;
v << fx_;
return v;
}
/* ************************************************************************* */
Point2 Cal3f::uncalibrate(const Point2& p, OptionalJacobian<2, 1> Dcal,
OptionalJacobian<2, 2> Dp) const {
assert(fx_ == fy_ && s_ == 0.0);
const double x = p.x(), y = p.y();
const double u = fx_ * x + u0_;
const double v = fx_ * y + v0_;
if (Dcal) {
Dcal->resize(2, 1);
(*Dcal) << x, y;
}
if (Dp) {
Dp->resize(2, 2);
(*Dp) << fx_, 0.0, //
0.0, fx_;
}
return Point2(u, v);
}
/* ************************************************************************* */
Point2 Cal3f::calibrate(const Point2& pi, OptionalJacobian<2, 1> Dcal,
OptionalJacobian<2, 2> Dp) const {
assert(fx_ == fy_ && s_ == 0.0);
const double u = pi.x(), v = pi.y();
double delta_u = u - u0_, delta_v = v - v0_;
double inv_f = 1.0 / fx_;
Point2 point(inv_f * delta_u, inv_f * delta_v);
if (Dcal) {
Dcal->resize(2, 1);
(*Dcal) << -inv_f * point.x(), -inv_f * point.y();
}
if (Dp) {
Dp->resize(2, 2);
(*Dp) << inv_f, 0.0, //
0.0, inv_f;
}
return point;
}
} // namespace gtsam

141
gtsam/geometry/Cal3f.h Normal file
View File

@ -0,0 +1,141 @@
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010, Georgia Tech Research Corporation,
* Atlanta, Georgia 30332-0415
* All Rights Reserved
* Authors: Frank Dellaert, et al. (see THANKS for the full author list)
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/**
* @file Cal3f.h
* @brief Calibration model with a single focal length and zero skew.
* @author Frank Dellaert
*/
#pragma once
#include <gtsam/geometry/Cal3.h>
namespace gtsam {
/**
* @brief Calibration model with a single focal length and zero skew.
* @ingroup geometry
* \nosubgrouping
*/
class GTSAM_EXPORT Cal3f : public Cal3 {
public:
enum { dimension = 1 };
using shared_ptr = std::shared_ptr<Cal3f>;
/// @name Constructors
/// @{
/// Default constructor
Cal3f() = default;
/**
* Constructor
* @param f focal length
* @param u0 image center x-coordinate (considered a constant)
* @param v0 image center y-coordinate (considered a constant)
*/
Cal3f(double f, double u0, double v0);
~Cal3f() override = default;
/// @}
/// @name Testable
/// @{
/// Output stream operator
GTSAM_EXPORT friend std::ostream& operator<<(std::ostream& os, const Cal3f& cal);
/// print with optional string
void print(const std::string& s = "") const override;
/// assert equality up to a tolerance
bool equals(const Cal3f& K, double tol = 1e-9) const;
/// @}
/// @name Standard Interface
/// @{
/// focal length
inline double f() const { return fx_; }
/// vectorized form (column-wise)
Vector1 vector() const;
/**
* @brief: convert intrinsic coordinates xy to image coordinates uv
* Version of uncalibrate with derivatives
* @param p point in intrinsic coordinates
* @param Dcal optional 2*1 Jacobian wrpt focal length
* @param Dp optional 2*2 Jacobian wrpt intrinsic coordinates
* @return point in image coordinates
*/
Point2 uncalibrate(const Point2& p, OptionalJacobian<2, 1> Dcal = {},
OptionalJacobian<2, 2> Dp = {}) const;
/**
* Convert a pixel coordinate to ideal coordinate xy
* @param pi point in image coordinates
* @param Dcal optional 2*1 Jacobian wrpt focal length
* @param Dp optional 2*2 Jacobian wrpt intrinsic coordinates
* @return point in intrinsic coordinates
*/
Point2 calibrate(const Point2& pi, OptionalJacobian<2, 1> Dcal = {},
OptionalJacobian<2, 2> Dp = {}) const;
/// @}
/// @name Manifold
/// @{
/// Return DOF, dimensionality of tangent space
size_t dim() const override { return Dim(); }
/// Return DOF, dimensionality of tangent space
inline static size_t Dim() { return dimension; }
/// Update calibration with tangent space delta
Cal3f retract(const Vector& d) const { return Cal3f(fx_ + d(0), u0_, v0_); }
/// Calculate local coordinates to another calibration
Vector1 localCoordinates(const Cal3f& T2) const {
return Vector1(T2.fx_ - fx_);
}
/// @}
private:
#ifdef GTSAM_ENABLE_BOOST_SERIALIZATION
/** Serialization function */
friend class boost::serialization::access;
template <class Archive>
void serialize(Archive& ar, const unsigned int /*version*/) {
ar& BOOST_SERIALIZATION_NVP(fx_);
ar& BOOST_SERIALIZATION_NVP(u0_);
ar& BOOST_SERIALIZATION_NVP(v0_);
}
#endif
/// @}
};
template <>
struct traits<Cal3f> : public internal::Manifold<Cal3f> {};
template <>
struct traits<const Cal3f> : public internal::Manifold<Cal3f> {};
} // namespace gtsam

67
gtsam/geometry/FundamentalMatrix.cpp
View File

@ -2,10 +2,12 @@
* @file FundamentalMatrix.cpp
* @brief FundamentalMatrix classes
* @author Frank Dellaert
* @date Oct 23, 2024
* @date October 2024
*/
#include <gtsam/base/Matrix.h>
#include <gtsam/geometry/FundamentalMatrix.h>
#include <gtsam/geometry/Point2.h>
namespace gtsam {
@ -26,6 +28,11 @@ Point2 EpipolarTransfer(const Matrix3& Fca, const Point2& pa, //
}
//*************************************************************************
FundamentalMatrix::FundamentalMatrix(const Matrix3& U, double s,
const Matrix3& V) {
initialize(U, s, V);
}
FundamentalMatrix::FundamentalMatrix(const Matrix3& F) {
// Perform SVD
Eigen::JacobiSVD<Matrix3> svd(F, Eigen::ComputeFullU | Eigen::ComputeFullV);
@ -47,28 +54,38 @@ FundamentalMatrix::FundamentalMatrix(const Matrix3& F) {
"The input matrix does not represent a valid fundamental matrix.");
}
// Ensure the second singular value is recorded as s
s_ = singularValues(1);
initialize(U, singularValues(1), V);
}
// Check if U is a reflection
if (U.determinant() < 0) {
U = -U;
s_ = -s_; // Change sign of scalar if U is a reflection
}
void FundamentalMatrix::initialize(Matrix3 U, double s, Matrix3 V) {
// Check if U is a reflection and flip third column if so
if (U.determinant() < 0) U.col(2) *= -1;
// Check if V is a reflection
if (V.determinant() < 0) {
V = -V;
s_ = -s_; // Change sign of scalar if U is a reflection
}
// Same check for V
if (V.determinant() < 0) V.col(2) *= -1;
// Assign the rotations
U_ = Rot3(U);
s_ = s;
V_ = Rot3(V);
}
Matrix3 FundamentalMatrix::matrix() const {
return U_.matrix() * Vector3(1, s_, 0).asDiagonal() * V_.transpose().matrix();
return U_.matrix() * Vector3(1.0, s_, 0).asDiagonal() *
V_.transpose().matrix();
}
Vector3 FundamentalMatrix::epipolarLine(const Point2& p,
OptionalJacobian<3, 7> H) {
Vector3 point(p.x(), p.y(), 1); // Create a point in homogeneous coordinates
Vector3 line = matrix() * point; // Compute the epipolar line
if (H) {
// Compute the Jacobian if requested
throw std::runtime_error(
"FundamentalMatrix::epipolarLine: Jacobian not implemented yet.");
}
return line; // Return the epipolar line
}
void FundamentalMatrix::print(const std::string& s) const {
@ -90,9 +107,9 @@ Vector FundamentalMatrix::localCoordinates(const FundamentalMatrix& F) const {
}
FundamentalMatrix FundamentalMatrix::retract(const Vector& delta) const {
Rot3 newU = U_.retract(delta.head<3>());
double newS = s_ + delta(3); // Update scalar
Rot3 newV = V_.retract(delta.tail<3>());
const Rot3 newU = U_.retract(delta.head<3>());
const double newS = s_ + delta(3);
const Rot3 newV = V_.retract(delta.tail<3>());
return FundamentalMatrix(newU, newS, newV);
}
@ -113,6 +130,20 @@ Matrix3 SimpleFundamentalMatrix::matrix() const {
return Ka().transpose().inverse() * E_.matrix() * Kb().inverse();
}
Vector3 SimpleFundamentalMatrix::epipolarLine(const Point2& p,
OptionalJacobian<3, 7> H) {
Vector3 point(p.x(), p.y(), 1); // Create a point in homogeneous coordinates
Vector3 line = matrix() * point; // Compute the epipolar line
if (H) {
// Compute the Jacobian if requested
throw std::runtime_error(
"SimpleFundamentalMatrix::epipolarLine: Jacobian not implemented yet.");
}
return line; // Return the epipolar line
}
void SimpleFundamentalMatrix::print(const std::string& s) const {
std::cout << s << " E:\n"
<< E_.matrix() << "\nfa: " << fa_ << "\nfb: " << fb_

64
gtsam/geometry/FundamentalMatrix.h
View File

@ -2,11 +2,12 @@
* @file FundamentalMatrix.h
* @brief FundamentalMatrix classes
* @author Frank Dellaert
* @date Oct 23, 2024
* @date October 2024
*/
#pragma once
#include <gtsam/base/OptionalJacobian.h>
#include <gtsam/geometry/EssentialMatrix.h>
#include <gtsam/geometry/Rot3.h>
#include <gtsam/geometry/Unit3.h>
@ -15,11 +16,15 @@ namespace gtsam {
/**
* @class FundamentalMatrix
* @brief Represents a general fundamental matrix.
* @brief Represents a fundamental matrix in computer vision, which encodes the
* epipolar geometry between two views.
*
* This class represents a general fundamental matrix, which is a 3x3 matrix
* that describes the relationship between two images. It is parameterized by a
* left rotation U, a scalar s, and a right rotation V.
* The FundamentalMatrix class encapsulates the fundamental matrix, which
* relates corresponding points in stereo images. It is parameterized by two
* rotation matrices (U and V) and a scalar parameter (s).
* Using these values, the fundamental matrix is represented as
*
* F = U * diag(1, s, 0) * V^T
*/
class GTSAM_EXPORT FundamentalMatrix {
private:
@ -34,15 +39,10 @@ class GTSAM_EXPORT FundamentalMatrix {
/**
* @brief Construct from U, V, and scalar s
*
* Initializes the FundamentalMatrix with the given left rotation U,
* scalar s, and right rotation V.
*
* @param U Left rotation matrix
* @param s Scalar parameter for the fundamental matrix
* @param V Right rotation matrix
* Initializes the FundamentalMatrix From the SVD representation
* U*diag(1,s,0)*V^T. It will internally convert to using SO(3).
*/
FundamentalMatrix(const Rot3& U, double s, const Rot3& V)
: U_(U), s_(s), V_(V) {}
FundamentalMatrix(const Matrix3& U, double s, const Matrix3& V);
/**
* @brief Construct from a 3x3 matrix using SVD
@ -54,26 +54,42 @@ class GTSAM_EXPORT FundamentalMatrix {
*/
FundamentalMatrix(const Matrix3& F);
/**
* @brief Construct from essential matrix and calibration matrices
*
* Initializes the FundamentalMatrix from the given essential matrix E
* and calibration matrices Ka and Kb, using
* F = Ka^(-T) * E * Kb^(-1)
* and then calls constructor that decomposes F via SVD.
*
* @param E Essential matrix
* @param Ka Calibration matrix for the left camera
* @param Kb Calibration matrix for the right camera
*/
FundamentalMatrix(const Matrix3& Ka, const EssentialMatrix& E,
const Matrix3& Kb)
: FundamentalMatrix(Ka.transpose().inverse() * E.matrix() *
Kb.inverse()) {}
/**
* @brief Construct from calibration matrices Ka, Kb, and pose aPb
*
* Initializes the FundamentalMatrix from the given calibration
* matrices Ka and Kb, and the pose aPb.
*
* @tparam CAL Calibration type, expected to have a matrix() method
* @param Ka Calibration matrix for the left camera
* @param aPb Pose from the left to the right camera
* @param Kb Calibration matrix for the right camera
*/
template <typename CAL>
FundamentalMatrix(const CAL& Ka, const Pose3& aPb, const CAL& Kb)
: FundamentalMatrix(Ka.K().transpose().inverse() *
EssentialMatrix::FromPose3(aPb).matrix() *
Kb.K().inverse()) {}
FundamentalMatrix(const Matrix3& Ka, const Pose3& aPb, const Matrix3& Kb)
: FundamentalMatrix(Ka, EssentialMatrix::FromPose3(aPb), Kb) {}
/// Return the fundamental matrix representation
Matrix3 matrix() const;
/// Computes the epipolar line in a (left) for a given point in b (right)
Vector3 epipolarLine(const Point2& p, OptionalJacobian<3, 7> H = {});
/// @name Testable
/// @{
/// Print the FundamentalMatrix
@ -96,6 +112,13 @@ class GTSAM_EXPORT FundamentalMatrix {
/// Retract the given vector to get a new FundamentalMatrix
FundamentalMatrix retract(const Vector& delta) const;
/// @}
private:
/// Private constructor for internal use
FundamentalMatrix(const Rot3& U, double s, const Rot3& V)
: U_(U), s_(s), V_(V) {}
/// Initialize SO(3) matrices from general O(3) matrices
void initialize(Matrix3 U, double s, Matrix3 V);
};
/**
@ -142,6 +165,9 @@ class GTSAM_EXPORT SimpleFundamentalMatrix {
/// F = Ka^(-T) * E * Kb^(-1)
Matrix3 matrix() const;
/// Computes the epipolar line in a (left) for a given point in b (right)
Vector3 epipolarLine(const Point2& p, OptionalJacobian<3, 7> H = {});
/// @name Testable
/// @{
/// Print the SimpleFundamentalMatrix

191
gtsam/geometry/geometry.i
View File

@ -360,6 +360,7 @@ class Rot3 {
// Standard Interface
static gtsam::Rot3 Expmap(gtsam::Vector v);
static gtsam::Vector Logmap(const gtsam::Rot3& p);
gtsam::Rot3 expmap(const gtsam::Vector& v);
gtsam::Vector logmap(const gtsam::Rot3& p);
gtsam::Matrix matrix() const;
gtsam::Matrix transpose() const;
@ -578,6 +579,8 @@ class Unit3 {
// Standard Constructors
Unit3();
Unit3(const gtsam::Point3& pose);
Unit3(double x, double y, double z);
Unit3(const gtsam::Point2& p, double f);
// Testable
void print(string s = "") const;
@ -620,10 +623,10 @@ class EssentialMatrix {
EssentialMatrix(const gtsam::Rot3& aRb, const gtsam::Unit3& aTb);
// Constructors from Pose3
gtsam::EssentialMatrix FromPose3(const gtsam::Pose3& _1P2_);
static gtsam::EssentialMatrix FromPose3(const gtsam::Pose3& _1P2_);
gtsam::EssentialMatrix FromPose3(const gtsam::Pose3& _1P2_,
Eigen::Ref<Eigen::MatrixXd> H);
static gtsam::EssentialMatrix FromPose3(const gtsam::Pose3& _1P2_,
Eigen::Ref<Eigen::MatrixXd> H);
// Testable
void print(string s = "") const;
@ -642,8 +645,36 @@ class EssentialMatrix {
double error(gtsam::Vector vA, gtsam::Vector vB);
};
#include <gtsam/geometry/Cal3.h>
virtual class Cal3 {
// Standard Constructors
Cal3();
Cal3(double fx, double fy, double s, double u0, double v0);
Cal3(gtsam::Vector v);
// Testable
void print(string s = "Cal3") const;
bool equals(const gtsam::Cal3& rhs, double tol) const;
// Standard Interface
double fx() const;
double fy() const;
double aspectRatio() const;
double skew() const;
double px() const;
double py() const;
gtsam::Point2 principalPoint() const;
gtsam::Vector vector() const;
gtsam::Matrix K() const;
gtsam::Matrix inverse() const;
// Manifold
static size_t Dim();
size_t dim() const;
};
#include <gtsam/geometry/Cal3_S2.h>
class Cal3_S2 {
virtual class Cal3_S2 : gtsam::Cal3 {
// Standard Constructors
Cal3_S2();
Cal3_S2(double fx, double fy, double s, double u0, double v0);
@ -670,23 +701,12 @@ class Cal3_S2 {
Eigen::Ref<Eigen::MatrixXd> Dcal,
Eigen::Ref<Eigen::MatrixXd> Dp) const;
// Standard Interface
double fx() const;
double fy() const;
double skew() const;
double px() const;
double py() const;
gtsam::Point2 principalPoint() const;
gtsam::Vector vector() const;
gtsam::Matrix K() const;
gtsam::Matrix inverse() const;
// enabling serialization functionality
void serialize() const;
};
#include <gtsam/geometry/Cal3DS2_Base.h>
virtual class Cal3DS2_Base {
virtual class Cal3DS2_Base : gtsam::Cal3 {
// Standard Constructors
Cal3DS2_Base();
@ -694,16 +714,8 @@ virtual class Cal3DS2_Base {
void print(string s = "") const;
// Standard Interface
double fx() const;
double fy() const;
double skew() const;
double px() const;
double py() const;
double k1() const;
double k2() const;
gtsam::Matrix K() const;
gtsam::Vector k() const;
gtsam::Vector vector() const;
// Action on Point2
gtsam::Point2 uncalibrate(const gtsam::Point2& p) const;
@ -783,7 +795,7 @@ virtual class Cal3Unified : gtsam::Cal3DS2_Base {
};
#include <gtsam/geometry/Cal3Fisheye.h>
class Cal3Fisheye {
virtual class Cal3Fisheye : gtsam::Cal3 {
// Standard Constructors
Cal3Fisheye();
Cal3Fisheye(double fx, double fy, double s, double u0, double v0, double k1,
@ -795,8 +807,6 @@ class Cal3Fisheye {
bool equals(const gtsam::Cal3Fisheye& rhs, double tol) const;
// Manifold
static size_t Dim();
size_t dim() const;
gtsam::Cal3Fisheye retract(gtsam::Vector v) const;
gtsam::Vector localCoordinates(const gtsam::Cal3Fisheye& c) const;
@ -811,35 +821,23 @@ class Cal3Fisheye {
Eigen::Ref<Eigen::MatrixXd> Dp) const;
// Standard Interface
double fx() const;
double fy() const;
double skew() const;
double k1() const;
double k2() const;
double k3() const;
double k4() const;
double px() const;
double py() const;
gtsam::Point2 principalPoint() const;
gtsam::Vector vector() const;
gtsam::Vector k() const;
gtsam::Matrix K() const;
gtsam::Matrix inverse() const;
// enabling serialization functionality
void serialize() const;
};
#include <gtsam/geometry/Cal3_S2Stereo.h>
class Cal3_S2Stereo {
virtual class Cal3_S2Stereo : gtsam::Cal3{
// Standard Constructors
Cal3_S2Stereo();
Cal3_S2Stereo(double fx, double fy, double s, double u0, double v0, double b);
Cal3_S2Stereo(gtsam::Vector v);
// Manifold
static size_t Dim();
size_t dim() const;
gtsam::Cal3_S2Stereo retract(gtsam::Vector v) const;
gtsam::Vector localCoordinates(const gtsam::Cal3_S2Stereo& c) const;
@ -848,35 +846,23 @@ class Cal3_S2Stereo {
bool equals(const gtsam::Cal3_S2Stereo& K, double tol) const;
// Standard Interface
double fx() const;
double fy() const;
double skew() const;
double px() const;
double py() const;
gtsam::Matrix K() const;
gtsam::Point2 principalPoint() const;
double baseline() const;
gtsam::Vector6 vector() const;
gtsam::Matrix inverse() const;
};
#include <gtsam/geometry/Cal3Bundler.h>
class Cal3Bundler {
virtual class Cal3f : gtsam::Cal3 {
// Standard Constructors
Cal3Bundler();
Cal3Bundler(double fx, double k1, double k2, double u0, double v0);
Cal3Bundler(double fx, double k1, double k2, double u0, double v0,
double tol);
Cal3f();
Cal3f(double fx, double u0, double v0);
// Testable
void print(string s = "") const;
bool equals(const gtsam::Cal3Bundler& rhs, double tol) const;
bool equals(const gtsam::Cal3f& rhs, double tol) const;
// Manifold
static size_t Dim();
size_t dim() const;
gtsam::Cal3Bundler retract(gtsam::Vector v) const;
gtsam::Vector localCoordinates(const gtsam::Cal3Bundler& c) const;
gtsam::Cal3f retract(gtsam::Vector v) const;
gtsam::Vector localCoordinates(const gtsam::Cal3f& c) const;
// Action on Point2
gtsam::Point2 calibrate(const gtsam::Point2& p) const;
@ -889,20 +875,90 @@ class Cal3Bundler {
Eigen::Ref<Eigen::MatrixXd> Dp) const;
// Standard Interface
double fx() const;
double fy() const;
double k1() const;
double k2() const;
double px() const;
double py() const;
gtsam::Vector vector() const;
gtsam::Vector k() const;
gtsam::Matrix K() const;
double f() const;
// enabling serialization functionality
void serialize() const;
};
#include <gtsam/geometry/Cal3Bundler.h>
virtual class Cal3Bundler : gtsam::Cal3f {
// Standard Constructors
Cal3Bundler();
Cal3Bundler(double fx, double k1, double k2, double u0, double v0);
Cal3Bundler(double fx, double k1, double k2, double u0, double v0,
double tol);
// Testable
void print(string s = "") const;
bool equals(const gtsam::Cal3Bundler& rhs, double tol) const;
// Manifold
gtsam::Cal3Bundler retract(gtsam::Vector v) const;
gtsam::Vector localCoordinates(const gtsam::Cal3Bundler& c) const;
// Standard Interface
double k1() const;
double k2() const;
// enabling serialization functionality
void serialize() const;
};
#include <gtsam/geometry/FundamentalMatrix.h>
// FundamentalMatrix class
class FundamentalMatrix {
// Constructors
FundamentalMatrix();
FundamentalMatrix(const gtsam::Matrix3& U, double s, const gtsam::Matrix3& V);
FundamentalMatrix(const gtsam::Matrix3& F);
// Overloaded constructors for specific calibration types
FundamentalMatrix(const gtsam::Matrix3& Ka, const gtsam::EssentialMatrix& E,
const gtsam::Matrix3& Kb);
FundamentalMatrix(const gtsam::Matrix3& Ka, const gtsam::Pose3& aPb,
const gtsam::Matrix3& Kb);
// Methods
gtsam::Matrix3 matrix() const;
// Testable
void print(const std::string& s = "") const;
bool equals(const gtsam::FundamentalMatrix& other, double tol = 1e-9) const;
// Manifold
static size_t Dim();
size_t dim() const;
gtsam::Vector localCoordinates(const gtsam::FundamentalMatrix& F) const;
gtsam::FundamentalMatrix retract(const gtsam::Vector& delta) const;
};
// SimpleFundamentalMatrix class
class SimpleFundamentalMatrix {
// Constructors
SimpleFundamentalMatrix();
SimpleFundamentalMatrix(const gtsam::EssentialMatrix& E, double fa, double fb,
const gtsam::Point2& ca, const gtsam::Point2& cb);
// Methods
gtsam::Matrix3 matrix() const;
// Testable
void print(const std::string& s = "") const;
bool equals(const gtsam::SimpleFundamentalMatrix& other, double tol = 1e-9) const;
// Manifold
static size_t Dim();
size_t dim() const;
gtsam::Vector localCoordinates(const gtsam::SimpleFundamentalMatrix& F) const;
gtsam::SimpleFundamentalMatrix retract(const gtsam::Vector& delta) const;
};
gtsam::Point2 EpipolarTransfer(const gtsam::Matrix3& Fca, const gtsam::Point2& pa,
const gtsam::Matrix3& Fcb, const gtsam::Point2& pb);
#include <gtsam/geometry/CalibratedCamera.h>
class CalibratedCamera {
// Standard Constructors and Named Constructors
@ -1016,6 +1072,7 @@ typedef gtsam::PinholeCamera<gtsam::Cal3_S2> PinholeCameraCal3_S2;
typedef gtsam::PinholeCamera<gtsam::Cal3DS2> PinholeCameraCal3DS2;
typedef gtsam::PinholeCamera<gtsam::Cal3Unified> PinholeCameraCal3Unified;
typedef gtsam::PinholeCamera<gtsam::Cal3Bundler> PinholeCameraCal3Bundler;
typedef gtsam::PinholeCamera<gtsam::Cal3f> PinholeCameraCal3f;
typedef gtsam::PinholeCamera<gtsam::Cal3Fisheye> PinholeCameraCal3Fisheye;
#include <gtsam/geometry/PinholePose.h>

40
gtsam/geometry/tests/testCal3Bundler.cpp
View File

@ -29,7 +29,7 @@ static Cal3Bundler K(500, 1e-3, 1e-3, 1000, 2000);
static Point2 p(2, 3);
/* ************************************************************************* */
TEST(Cal3Bundler, vector) {
TEST(Cal3Bundler, Vector) {
Cal3Bundler K;
Vector expected(3);
expected << 1, 0, 0;
@ -37,16 +37,19 @@ TEST(Cal3Bundler, vector) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, uncalibrate) {
TEST(Cal3Bundler, Uncalibrate) {
Vector v = K.vector();
double r = p.x() * p.x() + p.y() * p.y();
double g = v[0] * (1 + v[1] * r + v[2] * r * r);
Point2 expected(1000 + g * p.x(), 2000 + g * p.y());
double distortion = 1.0 + v[1] * r + v[2] * r * r;
double u = K.px() + v[0] * distortion * p.x();
double v_coord = K.py() + v[0] * distortion * p.y();
Point2 expected(u, v_coord);
Point2 actual = K.uncalibrate(p);
CHECK(assert_equal(expected, actual));
}
TEST(Cal3Bundler, calibrate) {
/* ************************************************************************* */
TEST(Cal3Bundler, Calibrate) {
Point2 pn(0.5, 0.5);
Point2 pi = K.uncalibrate(pn);
Point2 pn_hat = K.calibrate(pi);
@ -63,11 +66,11 @@ Point2 calibrate_(const Cal3Bundler& k, const Point2& pt) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, DuncalibrateDefault) {
TEST(Cal3Bundler, DUncalibrateDefault) {
Cal3Bundler trueK(1, 0, 0);
Matrix Dcal, Dp;
Point2 actual = trueK.uncalibrate(p, Dcal, Dp);
Point2 expected = p;
Point2 expected(p); // Since K is identity, uncalibrate should return p
CHECK(assert_equal(expected, actual, 1e-7));
Matrix numerical1 = numericalDerivative21(uncalibrate_, trueK, p);
Matrix numerical2 = numericalDerivative22(uncalibrate_, trueK, p);
@ -76,7 +79,7 @@ TEST(Cal3Bundler, DuncalibrateDefault) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, DcalibrateDefault) {
TEST(Cal3Bundler, DCalibrateDefault) {
Cal3Bundler trueK(1, 0, 0);
Matrix Dcal, Dp;
Point2 pn(0.5, 0.5);
@ -90,11 +93,11 @@ TEST(Cal3Bundler, DcalibrateDefault) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, DuncalibratePrincipalPoint) {
TEST(Cal3Bundler, DUncalibratePrincipalPoint) {
Cal3Bundler K(5, 0, 0, 2, 2);
Matrix Dcal, Dp;
Point2 actual = K.uncalibrate(p, Dcal, Dp);
Point2 expected(12, 17);
Point2 expected(2.0 + 5.0 * p.x(), 2.0 + 5.0 * p.y());
CHECK(assert_equal(expected, actual, 1e-7));
Matrix numerical1 = numericalDerivative21(uncalibrate_, K, p);
Matrix numerical2 = numericalDerivative22(uncalibrate_, K, p);
@ -103,7 +106,7 @@ TEST(Cal3Bundler, DuncalibratePrincipalPoint) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, DcalibratePrincipalPoint) {
TEST(Cal3Bundler, DCalibratePrincipalPoint) {
Cal3Bundler K(2, 0, 0, 2, 2);
Matrix Dcal, Dp;
Point2 pn(0.5, 0.5);
@ -117,11 +120,18 @@ TEST(Cal3Bundler, DcalibratePrincipalPoint) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, Duncalibrate) {
TEST(Cal3Bundler, DUncalibrate) {
Matrix Dcal, Dp;
Point2 actual = K.uncalibrate(p, Dcal, Dp);
Point2 expected(2182, 3773);
// Compute expected value manually
Vector v = K.vector();
double r2 = p.x() * p.x() + p.y() * p.y();
double distortion = 1.0 + v[1] * r2 + v[2] * r2 * r2;
Point2 expected(
K.px() + v[0] * distortion * p.x(),
K.py() + v[0] * distortion * p.y());
CHECK(assert_equal(expected, actual, 1e-7));
Matrix numerical1 = numericalDerivative21(uncalibrate_, K, p);
Matrix numerical2 = numericalDerivative22(uncalibrate_, K, p);
CHECK(assert_equal(numerical1, Dcal, 1e-7));
@ -129,7 +139,7 @@ TEST(Cal3Bundler, Duncalibrate) {
}
/* ************************************************************************* */
TEST(Cal3Bundler, Dcalibrate) {
TEST(Cal3Bundler, DCalibrate) {
Matrix Dcal, Dp;
Point2 pn(0.5, 0.5);
Point2 pi = K.uncalibrate(pn);
@ -145,7 +155,7 @@ TEST(Cal3Bundler, Dcalibrate) {
TEST(Cal3Bundler, assert_equal) { CHECK(assert_equal(K, K, 1e-7)); }
/* ************************************************************************* */
TEST(Cal3Bundler, retract) {
TEST(Cal3Bundler, Retract) {
Cal3Bundler expected(510, 2e-3, 2e-3, 1000, 2000);
EXPECT_LONGS_EQUAL(3, expected.dim());

132
gtsam/geometry/tests/testCal3f.cpp Normal file
View File

@ -0,0 +1,132 @@
/* ----------------------------------------------------------------------------
* GTSAM Copyright 2010, Georgia Tech Research Corporation,
* Atlanta, Georgia 30332-0415
* All Rights Reserved
* Authors: Frank Dellaert, et al. (see THANKS for the full author list)
* See LICENSE for the license information
* -------------------------------------------------------------------------- */
/**
* @file testCal3F.cpp
* @brief Unit tests for the Cal3f calibration model.
*/
#include <CppUnitLite/TestHarness.h>
#include <gtsam/base/Testable.h>
#include <gtsam/base/TestableAssertions.h>
#include <gtsam/base/numericalDerivative.h>
#include <gtsam/geometry/Cal3f.h>
using namespace gtsam;
GTSAM_CONCEPT_TESTABLE_INST(Cal3f)
GTSAM_CONCEPT_MANIFOLD_INST(Cal3f)
static Cal3f K(500.0, 1000.0, 2000.0); // f = 500, u0 = 1000, v0 = 2000
static Point2 p(2.0, 3.0);
/* ************************************************************************* */
TEST(Cal3f, Vector) {
Cal3f K(1.0, 0.0, 0.0);
Vector expected(1);
expected << 1.0;
CHECK(assert_equal(expected, K.vector()));
}
/* ************************************************************************* */
TEST(Cal3f, Uncalibrate) {
// Expected output: apply the intrinsic calibration matrix to point p
Matrix3 K_matrix = K.K();
Vector3 p_homogeneous(p.x(), p.y(), 1.0);
Vector3 expected_homogeneous = K_matrix * p_homogeneous;
Point2 expected(expected_homogeneous.x() / expected_homogeneous.z(),
expected_homogeneous.y() / expected_homogeneous.z());
Point2 actual = K.uncalibrate(p);
CHECK(assert_equal(expected, actual));
}
/* ************************************************************************* */
TEST(Cal3f, Calibrate) {
Point2 pi = K.uncalibrate(p);
Point2 pn = K.calibrate(pi);
CHECK(traits<Point2>::Equals(p, pn, 1e-9));
}
/* ************************************************************************* */
Point2 uncalibrate_(const Cal3f& k, const Point2& pt) {
return k.uncalibrate(pt);
}
Point2 calibrate_(const Cal3f& k, const Point2& pt) { return k.calibrate(pt); }
/* ************************************************************************* */
TEST(Cal3f, DUncalibrate) {
Cal3f K(500.0, 1000.0, 2000.0);
Matrix Dcal, Dp;
Point2 actual = K.uncalibrate(p, Dcal, Dp);
// Expected value computed manually
Point2 expected = Point2(K.px() + K.fx() * p.x(), K.py() + K.fx() * p.y());
CHECK(assert_equal(expected, actual, 1e-9));
// Compute numerical derivatives
Matrix numerical1 = numericalDerivative21(uncalibrate_, K, p);
Matrix numerical2 = numericalDerivative22(uncalibrate_, K, p);
CHECK(assert_equal(numerical1, Dcal, 1e-6));
CHECK(assert_equal(numerical2, Dp, 1e-6));
}
/* ************************************************************************* */
TEST(Cal3f, DCalibrate) {
Point2 pi = K.uncalibrate(p);
Matrix Dcal, Dp;
Point2 actual = K.calibrate(pi, Dcal, Dp);
CHECK(assert_equal(p, actual, 1e-9));
// Compute numerical derivatives
Matrix numerical1 = numericalDerivative21(calibrate_, K, pi);
Matrix numerical2 = numericalDerivative22(calibrate_, K, pi);
CHECK(assert_equal(numerical1, Dcal, 1e-6));
CHECK(assert_equal(numerical2, Dp, 1e-6));
}
/* ************************************************************************* */
TEST(Cal3f, Manifold) {
Cal3f K1(500.0, 1000.0, 2000.0);
Vector1 delta;
delta << 10.0; // Increment focal length by 10
Cal3f K2 = K1.retract(delta);
CHECK(assert_equal(510.0, K2.fx(), 1e-9));
CHECK(assert_equal(K1.px(), K2.px(), 1e-9));
CHECK(assert_equal(K1.py(), K2.py(), 1e-9));
Vector1 delta_computed = K1.localCoordinates(K2);
CHECK(assert_equal(delta, delta_computed, 1e-9));
}
/* ************************************************************************* */
TEST(Cal3f, Assert_equal) {
CHECK(assert_equal(K, K, 1e-9));
Cal3f K2(500.0, 1000.0, 2000.0);
CHECK(assert_equal(K, K2, 1e-9));
}
/* ************************************************************************* */
TEST(Cal3f, Print) {
Cal3f cal(500.0, 1000.0, 2000.0);
std::stringstream os;
os << "f: " << cal.fx() << ", px: " << cal.px() << ", py: " << cal.py();
EXPECT(assert_stdout_equal(os.str(), cal));
}
/* ************************************************************************* */
int main() {
TestResult tr;
return TestRegistry::runAllTests(tr);
}
/* ************************************************************************* */

30
gtsam/geometry/tests/testFundamentalMatrix.cpp
View File

@ -6,12 +6,15 @@
*/
#include <CppUnitLite/TestHarness.h>
#include <gtsam/base/Matrix.h>
#include <gtsam/base/Testable.h>
#include <gtsam/geometry/FundamentalMatrix.h>
#include <gtsam/geometry/Rot3.h>
#include <gtsam/geometry/SimpleCamera.h>
#include <gtsam/geometry/Unit3.h>
#include <cmath>
using namespace std::placeholders;
using namespace std;
using namespace gtsam;
@ -24,21 +27,38 @@ GTSAM_CONCEPT_MANIFOLD_INST(FundamentalMatrix)
Rot3 trueU = Rot3::Yaw(M_PI_2);
Rot3 trueV = Rot3::Yaw(M_PI_4);
double trueS = 0.5;
FundamentalMatrix trueF(trueU, trueS, trueV);
FundamentalMatrix trueF(trueU.matrix(), trueS, trueV.matrix());
//*************************************************************************
TEST(FundamentalMatrix, localCoordinates) {
TEST(FundamentalMatrix, LocalCoordinates) {
Vector expected = Z_7x1; // Assuming 7 dimensions for U, V, and s
Vector actual = trueF.localCoordinates(trueF);
EXPECT(assert_equal(expected, actual, 1e-8));
}
//*************************************************************************
TEST(FundamentalMatrix, retract) {
TEST(FundamentalMatrix, Retract) {
FundamentalMatrix actual = trueF.retract(Z_7x1);
EXPECT(assert_equal(trueF, actual));
}
//*************************************************************************
// Test conversion from F matrices, including non-rotations
TEST(FundamentalMatrix, Conversion) {
Matrix3 U = trueU.matrix();
Matrix3 V = trueV.matrix();
std::vector<FundamentalMatrix> Fs = {
FundamentalMatrix(U, trueS, V), FundamentalMatrix(U, trueS, -V),
FundamentalMatrix(-U, trueS, V), FundamentalMatrix(-U, trueS, -V)};
for (const auto& trueF : Fs) {
const Matrix3 F = trueF.matrix();
FundamentalMatrix actual(F);
// We check the matrices as the underlying representation is not unique
CHECK(assert_equal(F, actual.matrix()));
}
}
//*************************************************************************
TEST(FundamentalMatrix, RoundTrip) {
Vector7 d;
@ -61,14 +81,14 @@ TEST(SimpleStereo, Conversion) {
}
//*************************************************************************
TEST(SimpleStereo, localCoordinates) {
TEST(SimpleStereo, LocalCoordinates) {
Vector expected = Z_7x1;
Vector actual = stereoF.localCoordinates(stereoF);
EXPECT(assert_equal(expected, actual, 1e-8));
}
//*************************************************************************
TEST(SimpleStereo, retract) {
TEST(SimpleStereo, Retract) {
SimpleFundamentalMatrix actual = stereoF.retract(Z_9x1);
EXPECT(assert_equal(stereoF, actual));
}

24
gtsam/hybrid/HybridBayesNet.cpp
View File

@ -197,6 +197,30 @@ AlgebraicDecisionTree<Key> HybridBayesNet::errorTree(
return result;
}
/* ************************************************************************* */
double HybridBayesNet::negLogConstant(
const std::optional<DiscreteValues> &discrete) const {
double negLogNormConst = 0.0;
// Iterate over each conditional.
for (auto &&conditional : *this) {
if (discrete.has_value()) {
if (auto gm = conditional->asHybrid()) {
negLogNormConst += gm->choose(*discrete)->negLogConstant();
} else if (auto gc = conditional->asGaussian()) {
negLogNormConst += gc->negLogConstant();
} else if (auto dc = conditional->asDiscrete()) {
negLogNormConst += dc->choose(*discrete)->negLogConstant();
} else {
throw std::runtime_error(
"Unknown conditional type when computing negLogConstant");
}
} else {
negLogNormConst += conditional->negLogConstant();
}
}
return negLogNormConst;
}
/* ************************************************************************* */
AlgebraicDecisionTree<Key> HybridBayesNet::discretePosterior(
const VectorValues &continuousValues) const {

10
gtsam/hybrid/HybridBayesNet.h
View File

@ -237,6 +237,16 @@ class GTSAM_EXPORT HybridBayesNet : public BayesNet<HybridConditional> {
using BayesNet::logProbability; // expose HybridValues version
/**
* @brief Get the negative log of the normalization constant
* corresponding to the joint density represented by this Bayes net.
* Optionally index by `discrete`.
*
* @param discrete Optional DiscreteValues
* @return double
*/
double negLogConstant(const std::optional<DiscreteValues> &discrete) const;
/**
* @brief Compute normalized posterior P(M|X=x) and return as a tree.
*

8
gtsam/hybrid/HybridBayesTree.cpp
View File

@ -210,9 +210,11 @@ void HybridBayesTree::prune(const size_t maxNrLeaves) {
if (conditional->isHybrid()) {
auto hybridGaussianCond = conditional->asHybrid();
// Imperative
clique->conditional() = std::make_shared<HybridConditional>(
hybridGaussianCond->prune(parentData.prunedDiscreteProbs));
if (!hybridGaussianCond->pruned()) {
// Imperative
clique->conditional() = std::make_shared<HybridConditional>(
hybridGaussianCond->prune(parentData.prunedDiscreteProbs));
}
}
return parentData;
}

19
gtsam/hybrid/HybridGaussianConditional.cpp
View File

@ -120,7 +120,7 @@ struct HybridGaussianConditional::Helper {
/* *******************************************************************************/
HybridGaussianConditional::HybridGaussianConditional(
const DiscreteKeys &discreteParents, Helper &&helper)
const DiscreteKeys &discreteParents, Helper &&helper, bool pruned)
: BaseFactor(discreteParents,
FactorValuePairs(
[&](const GaussianFactorValuePair
@ -130,7 +130,8 @@ HybridGaussianConditional::HybridGaussianConditional(
},
std::move(helper.pairs))),
BaseConditional(*helper.nrFrontals),
negLogConstant_(helper.minNegLogConstant) {}
negLogConstant_(helper.minNegLogConstant),
pruned_(pruned) {}
HybridGaussianConditional::HybridGaussianConditional(
const DiscreteKey &discreteParent,
@ -166,8 +167,9 @@ HybridGaussianConditional::HybridGaussianConditional(
: HybridGaussianConditional(discreteParents, Helper(conditionals)) {}
HybridGaussianConditional::HybridGaussianConditional(
const DiscreteKeys &discreteParents, const FactorValuePairs &pairs)
: HybridGaussianConditional(discreteParents, Helper(pairs)) {}
const DiscreteKeys &discreteParents, const FactorValuePairs &pairs,
bool pruned)
: HybridGaussianConditional(discreteParents, Helper(pairs), pruned) {}
/* *******************************************************************************/
const HybridGaussianConditional::Conditionals
@ -322,13 +324,16 @@ HybridGaussianConditional::shared_ptr HybridGaussianConditional::prune(
const GaussianFactorValuePair &pair) -> GaussianFactorValuePair {
if (max->evaluate(choices) == 0.0)
return {nullptr, std::numeric_limits<double>::infinity()};
else
return pair;
else {
// Add negLogConstant_ back so that the minimum negLogConstant in the
// HybridGaussianConditional is set correctly.
return {pair.first, pair.second + negLogConstant_};
}
};
FactorValuePairs prunedConditionals = factors().apply(pruner);
return std::make_shared<HybridGaussianConditional>(discreteKeys(),
prunedConditionals);
prunedConditionals, true);
}
/* *******************************************************************************/

11
gtsam/hybrid/HybridGaussianConditional.h
View File

@ -68,6 +68,9 @@ class GTSAM_EXPORT HybridGaussianConditional
///< Take advantage of the neg-log space so everything is a minimization
double negLogConstant_;
/// Flag to indicate if the conditional has been pruned.
bool pruned_ = false;
public:
/// @name Constructors
/// @{
@ -150,9 +153,10 @@ class GTSAM_EXPORT HybridGaussianConditional
*
* @param discreteParents the discrete parents. Will be placed last.
* @param conditionalPairs Decision tree of GaussianFactor/scalar pairs.
* @param pruned Flag indicating if conditional has been pruned.
*/
HybridGaussianConditional(const DiscreteKeys &discreteParents,
const FactorValuePairs &pairs);
const FactorValuePairs &pairs, bool pruned = false);
/// @}
/// @name Testable
@ -233,6 +237,9 @@ class GTSAM_EXPORT HybridGaussianConditional
HybridGaussianConditional::shared_ptr prune(
const DecisionTreeFactor &discreteProbs) const;
/// Return true if the conditional has already been pruned.
bool pruned() const { return pruned_; }
/// @}
private:
@ -241,7 +248,7 @@ class GTSAM_EXPORT HybridGaussianConditional
/// Private constructor that uses helper struct above.
HybridGaussianConditional(const DiscreteKeys &discreteParents,
Helper &&helper);
Helper &&helper, bool pruned = false);
/// Check whether `given` has values for all frontal keys.
bool allFrontalsGiven(const VectorValues &given) const;

1
gtsam/hybrid/HybridGaussianFactor.h
View File

@ -148,6 +148,7 @@ class GTSAM_EXPORT HybridGaussianFactor : public HybridFactor {
/// Getter for GaussianFactor decision tree
const FactorValuePairs &factors() const { return factors_; }
/**
* @brief Helper function to return factors and functional to create a
* DecisionTree of Gaussian Factor Graphs.

18
gtsam/hybrid/HybridGaussianFactorGraph.cpp
View File

@ -59,10 +59,11 @@ using OrphanWrapper = BayesTreeOrphanWrapper<HybridBayesTree::Clique>;
/// Result from elimination.
struct Result {
// Gaussian conditional resulting from elimination.
GaussianConditional::shared_ptr conditional;
double negLogK;
GaussianFactor::shared_ptr factor;
double scalar;
double negLogK; // Negative log of the normalization constant K.
GaussianFactor::shared_ptr factor; // Leftover factor 𝜏.
double scalar; // Scalar value associated with factor 𝜏.
bool operator==(const Result &other) const {
return conditional == other.conditional && negLogK == other.negLogK &&
@ -580,4 +581,15 @@ GaussianFactorGraph HybridGaussianFactorGraph::choose(
return gfg;
}
/* ************************************************************************ */
DiscreteFactorGraph HybridGaussianFactorGraph::discreteFactors() const {
DiscreteFactorGraph dfg;
for (auto &&f : factors_) {
if (auto discreteFactor = std::dynamic_pointer_cast<DiscreteFactor>(f)) {
dfg.push_back(discreteFactor);
}
}
return dfg;
}
} // namespace gtsam

9
gtsam/hybrid/HybridGaussianFactorGraph.h
View File

@ -18,6 +18,7 @@
#pragma once
#include <gtsam/discrete/DiscreteFactorGraph.h>
#include <gtsam/discrete/DiscreteKey.h>
#include <gtsam/hybrid/HybridFactor.h>
#include <gtsam/hybrid/HybridFactorGraph.h>
@ -254,6 +255,14 @@ class GTSAM_EXPORT HybridGaussianFactorGraph
GaussianFactorGraph operator()(const DiscreteValues& assignment) const {
return choose(assignment);
}
/**
* @brief Helper method to get all the discrete factors
* as a DiscreteFactorGraph.
*
* @return DiscreteFactorGraph
*/
DiscreteFactorGraph discreteFactors() const;
};
// traits

38
gtsam/hybrid/HybridNonlinearFactor.cpp
View File

@ -16,6 +16,7 @@
* @date Sep 12, 2024
*/
#include <gtsam/discrete/DecisionTreeFactor.h>
#include <gtsam/hybrid/HybridNonlinearFactor.h>
#include <gtsam/linear/NoiseModel.h>
#include <gtsam/nonlinear/NonlinearFactor.h>
@ -184,6 +185,11 @@ std::shared_ptr<HybridGaussianFactor> HybridNonlinearFactor::linearize(
[continuousValues](
const std::pair<sharedFactor, double>& f) -> GaussianFactorValuePair {
auto [factor, val] = f;
// Check if valid factor. If not, return null and infinite error.
if (!factor) {
return {nullptr, std::numeric_limits<double>::infinity()};
}
if (auto gaussian = std::dynamic_pointer_cast<noiseModel::Gaussian>(
factor->noiseModel())) {
return {factor->linearize(continuousValues),
@ -202,4 +208,34 @@ std::shared_ptr<HybridGaussianFactor> HybridNonlinearFactor::linearize(
linearized_factors);
}
} // namespace gtsam
/* *******************************************************************************/
HybridNonlinearFactor::shared_ptr HybridNonlinearFactor::prune(
const DecisionTreeFactor& discreteProbs) const {
// Find keys in discreteProbs.keys() but not in this->keys():
std::set<Key> mine(this->keys().begin(), this->keys().end());
std::set<Key> theirs(discreteProbs.keys().begin(),
discreteProbs.keys().end());
std::vector<Key> diff;
std::set_difference(theirs.begin(), theirs.end(), mine.begin(), mine.end(),
std::back_inserter(diff));
// Find maximum probability value for every combination of our keys.
Ordering keys(diff);
auto max = discreteProbs.max(keys);
// Check the max value for every combination of our keys.
// If the max value is 0.0, we can prune the corresponding conditional.
auto pruner =
[&](const Assignment<Key>& choices,
const NonlinearFactorValuePair& pair) -> NonlinearFactorValuePair {
if (max->evaluate(choices) == 0.0)
return {nullptr, std::numeric_limits<double>::infinity()};
else
return pair;
};
FactorValuePairs prunedFactors = factors().apply(pruner);
return std::make_shared<HybridNonlinearFactor>(discreteKeys(), prunedFactors);
}
} // namespace gtsam

7
gtsam/hybrid/HybridNonlinearFactor.h
View File

@ -166,6 +166,9 @@ class GTSAM_EXPORT HybridNonlinearFactor : public HybridFactor {
/// @}
/// Getter for NonlinearFactor decision tree
const FactorValuePairs& factors() const { return factors_; }
/// Linearize specific nonlinear factors based on the assignment in
/// discreteValues.
GaussianFactor::shared_ptr linearize(
@ -176,6 +179,10 @@ class GTSAM_EXPORT HybridNonlinearFactor : public HybridFactor {
std::shared_ptr<HybridGaussianFactor> linearize(
const Values& continuousValues) const;
/// Prune this factor based on the discrete probabilities.
HybridNonlinearFactor::shared_ptr prune(
const DecisionTreeFactor& discreteProbs) const;
private:
/// Helper struct to assist private constructor below.
struct ConstructorHelper;

15
gtsam/hybrid/HybridNonlinearISAM.cpp
View File

@ -16,6 +16,7 @@
*/
#include <gtsam/hybrid/HybridGaussianFactorGraph.h>
#include <gtsam/hybrid/HybridNonlinearFactor.h>
#include <gtsam/hybrid/HybridNonlinearISAM.h>
#include <gtsam/inference/Ordering.h>
@ -39,7 +40,6 @@ void HybridNonlinearISAM::update(const HybridNonlinearFactorGraph& newFactors,
if (newFactors.size() > 0) {
// Reorder and relinearize every reorderInterval updates
if (reorderInterval_ > 0 && ++reorderCounter_ >= reorderInterval_) {
// TODO(Varun) Re-linearization doesn't take into account pruning
reorderRelinearize();
reorderCounter_ = 0;
}
@ -65,8 +65,21 @@ void HybridNonlinearISAM::reorderRelinearize() {
// Obtain the new linearization point
const Values newLinPoint = estimate();
auto discreteProbs = *(isam_.roots().at(0)->conditional()->asDiscrete());
isam_.clear();
// Prune nonlinear factors based on discrete conditional probabilities
HybridNonlinearFactorGraph pruned_factors;
for (auto&& factor : factors_) {
if (auto nf = std::dynamic_pointer_cast<HybridNonlinearFactor>(factor)) {
pruned_factors.push_back(nf->prune(discreteProbs));
} else {
pruned_factors.push_back(factor);
}
}
factors_ = pruned_factors;
// Just recreate the whole BayesTree
// TODO: allow for constrained ordering here
// TODO: decouple re-linearization and reordering to avoid

51
gtsam/hybrid/tests/Switching.h
View File

@ -52,7 +52,8 @@ using symbol_shorthand::X;
* @return HybridGaussianFactorGraph::shared_ptr
*/
inline HybridGaussianFactorGraph::shared_ptr makeSwitchingChain(
size_t K, std::function<Key(int)> x = X, std::function<Key(int)> m = M) {
size_t K, std::function<Key(int)> x = X, std::function<Key(int)> m = M,
const std::string &transitionProbabilityTable = "0 1 1 3") {
HybridGaussianFactorGraph hfg;
hfg.add(JacobianFactor(x(1), I_3x3, Z_3x1));
@ -68,7 +69,8 @@ inline HybridGaussianFactorGraph::shared_ptr makeSwitchingChain(
hfg.add(HybridGaussianFactor({m(k), 2}, components));
if (k > 1) {
hfg.add(DecisionTreeFactor({{m(k - 1), 2}, {m(k), 2}}, "0 1 1 3"));
hfg.add(DecisionTreeFactor({{m(k - 1), 2}, {m(k), 2}},
transitionProbabilityTable));
}
}
@ -120,21 +122,13 @@ using MotionModel = BetweenFactor<double>;
// Test fixture with switching network.
/// ϕ(X(0)) .. ϕ(X(k),X(k+1)) .. ϕ(X(k);z_k) .. ϕ(M(0)) .. ϕ(M(K-3),M(K-2))
struct Switching {
private:
HybridNonlinearFactorGraph nonlinearFactorGraph_;
public:
size_t K;
DiscreteKeys modes;
HybridNonlinearFactorGraph unaryFactors, binaryFactors, modeChain;
HybridGaussianFactorGraph linearizedFactorGraph;
HybridGaussianFactorGraph linearUnaryFactors, linearBinaryFactors;
Values linearizationPoint;
// Access the flat nonlinear factor graph.
const HybridNonlinearFactorGraph &nonlinearFactorGraph() const {
return nonlinearFactorGraph_;
}
/**
* @brief Create with given number of time steps.
*
@ -164,36 +158,33 @@ struct Switching {
// Create hybrid factor graph.
// Add a prior ϕ(X(0)) on X(0).
nonlinearFactorGraph_.emplace_shared<PriorFactor<double>>(
unaryFactors.emplace_shared<PriorFactor<double>>(
X(0), measurements.at(0), Isotropic::Sigma(1, prior_sigma));
unaryFactors.push_back(nonlinearFactorGraph_.back());
// Add "motion models" ϕ(X(k),X(k+1),M(k)).
for (size_t k = 0; k < K - 1; k++) {
auto motion_models = motionModels(k, between_sigma);
nonlinearFactorGraph_.emplace_shared<HybridNonlinearFactor>(modes[k],
motion_models);
binaryFactors.push_back(nonlinearFactorGraph_.back());
binaryFactors.emplace_shared<HybridNonlinearFactor>(modes[k],
motion_models);
}
// Add measurement factors ϕ(X(k);z_k).
auto measurement_noise = Isotropic::Sigma(1, prior_sigma);
for (size_t k = 1; k < K; k++) {
nonlinearFactorGraph_.emplace_shared<PriorFactor<double>>(
X(k), measurements.at(k), measurement_noise);
unaryFactors.push_back(nonlinearFactorGraph_.back());
unaryFactors.emplace_shared<PriorFactor<double>>(X(k), measurements.at(k),
measurement_noise);
}
// Add "mode chain" ϕ(M(0)) ϕ(M(0),M(1)) ... ϕ(M(K-3),M(K-2))
modeChain = createModeChain(transitionProbabilityTable);
nonlinearFactorGraph_ += modeChain;
// Create the linearization point.
for (size_t k = 0; k < K; k++) {
linearizationPoint.insert<double>(X(k), static_cast<double>(k + 1));
}
linearizedFactorGraph = *nonlinearFactorGraph_.linearize(linearizationPoint);
linearUnaryFactors = *unaryFactors.linearize(linearizationPoint);
linearBinaryFactors = *binaryFactors.linearize(linearizationPoint);
}
// Create motion models for a given time step
@ -224,6 +215,24 @@ struct Switching {
}
return chain;
}
/// Get the full linear factor graph.
HybridGaussianFactorGraph linearizedFactorGraph() const {
HybridGaussianFactorGraph graph;
graph.push_back(linearUnaryFactors);
graph.push_back(linearBinaryFactors);
graph.push_back(modeChain);
return graph;
}
/// Get all the nonlinear factors.
HybridNonlinearFactorGraph nonlinearFactorGraph() const {
HybridNonlinearFactorGraph graph;
graph.push_back(unaryFactors);
graph.push_back(binaryFactors);
graph.push_back(modeChain);
return graph;
}
};
} // namespace gtsam

55
gtsam/hybrid/tests/testHybridBayesNet.cpp
View File

@ -31,6 +31,7 @@
// Include for test suite
#include <CppUnitLite/TestHarness.h>
#include <memory>
using namespace std;
@ -263,7 +264,7 @@ TEST(HybridBayesNet, Choose) {
const Ordering ordering(s.linearizationPoint.keys());
const auto [hybridBayesNet, remainingFactorGraph] =
s.linearizedFactorGraph.eliminatePartialSequential(ordering);
s.linearizedFactorGraph().eliminatePartialSequential(ordering);
DiscreteValues assignment;
assignment[M(0)] = 1;
@ -292,7 +293,7 @@ TEST(HybridBayesNet, OptimizeAssignment) {
const Ordering ordering(s.linearizationPoint.keys());
const auto [hybridBayesNet, remainingFactorGraph] =
s.linearizedFactorGraph.eliminatePartialSequential(ordering);
s.linearizedFactorGraph().eliminatePartialSequential(ordering);
DiscreteValues assignment;
assignment[M(0)] = 1;
@ -319,7 +320,7 @@ TEST(HybridBayesNet, Optimize) {
Switching s(4, 1.0, 0.1, {0, 1, 2, 3}, "1/1 1/1");
HybridBayesNet::shared_ptr hybridBayesNet =
s.linearizedFactorGraph.eliminateSequential();
s.linearizedFactorGraph().eliminateSequential();
HybridValues delta = hybridBayesNet->optimize();
@ -347,7 +348,7 @@ TEST(HybridBayesNet, Pruning) {
Switching s(3);
HybridBayesNet::shared_ptr posterior =
s.linearizedFactorGraph.eliminateSequential();
s.linearizedFactorGraph().eliminateSequential();
EXPECT_LONGS_EQUAL(5, posterior->size());
// Optimize
@ -362,10 +363,6 @@ TEST(HybridBayesNet, Pruning) {
AlgebraicDecisionTree<Key> expected(s.modes, leaves);
EXPECT(assert_equal(expected, discretePosterior, 1e-6));
// Prune and get probabilities
auto prunedBayesNet = posterior->prune(2);
auto prunedTree = prunedBayesNet.discretePosterior(delta.continuous());
// Verify logProbability computation and check specific logProbability value
const DiscreteValues discrete_values{{M(0), 1}, {M(1), 1}};
const HybridValues hybridValues{delta.continuous(), discrete_values};
@ -380,10 +377,21 @@ TEST(HybridBayesNet, Pruning) {
EXPECT_DOUBLES_EQUAL(logProbability, posterior->logProbability(hybridValues),
1e-9);
double negLogConstant = posterior->negLogConstant(discrete_values);
// The sum of all the mode densities
double normalizer =
AlgebraicDecisionTree<Key>(posterior->errorTree(delta.continuous()),
[](double error) { return exp(-error); })
.sum();
// Check agreement with discrete posterior
// double density = exp(logProbability);
// FAILS: EXPECT_DOUBLES_EQUAL(density, discretePosterior(discrete_values),
// 1e-6);
double density = exp(logProbability + negLogConstant) / normalizer;
EXPECT_DOUBLES_EQUAL(density, discretePosterior(discrete_values), 1e-6);
// Prune and get probabilities
auto prunedBayesNet = posterior->prune(2);
auto prunedTree = prunedBayesNet.discretePosterior(delta.continuous());
// Regression test on pruned logProbability tree
std::vector<double> pruned_leaves = {0.0, 0.50758422, 0.0, 0.49241578};
@ -391,7 +399,26 @@ TEST(HybridBayesNet, Pruning) {
EXPECT(assert_equal(expected_pruned, prunedTree, 1e-6));
// Regression
// FAILS: EXPECT_DOUBLES_EQUAL(density, prunedTree(discrete_values), 1e-9);
double pruned_logProbability = 0;
pruned_logProbability +=
prunedBayesNet.at(0)->asDiscrete()->logProbability(hybridValues);
pruned_logProbability +=
prunedBayesNet.at(1)->asHybrid()->logProbability(hybridValues);
pruned_logProbability +=
prunedBayesNet.at(2)->asHybrid()->logProbability(hybridValues);
pruned_logProbability +=
prunedBayesNet.at(3)->asHybrid()->logProbability(hybridValues);
double pruned_negLogConstant = prunedBayesNet.negLogConstant(discrete_values);
// The sum of all the mode densities
double pruned_normalizer =
AlgebraicDecisionTree<Key>(prunedBayesNet.errorTree(delta.continuous()),
[](double error) { return exp(-error); })
.sum();
double pruned_density =
exp(pruned_logProbability + pruned_negLogConstant) / pruned_normalizer;
EXPECT_DOUBLES_EQUAL(pruned_density, prunedTree(discrete_values), 1e-9);
}
/* ****************************************************************************/
@ -400,7 +427,7 @@ TEST(HybridBayesNet, Prune) {
Switching s(4);
HybridBayesNet::shared_ptr posterior =
s.linearizedFactorGraph.eliminateSequential();
s.linearizedFactorGraph().eliminateSequential();
EXPECT_LONGS_EQUAL(7, posterior->size());
HybridValues delta = posterior->optimize();
@ -418,7 +445,7 @@ TEST(HybridBayesNet, UpdateDiscreteConditionals) {
Switching s(4);
HybridBayesNet::shared_ptr posterior =
s.linearizedFactorGraph.eliminateSequential();
s.linearizedFactorGraph().eliminateSequential();
EXPECT_LONGS_EQUAL(7, posterior->size());
DiscreteConditional joint;

144
gtsam/hybrid/tests/testHybridBayesTree.cpp
View File

@ -74,9 +74,7 @@ TEST(HybridGaussianFactorGraph,
hfg.add(HybridGaussianFactor(m1, two::components(X(1))));
hfg.add(DecisionTreeFactor(m1, {2, 8}));
// TODO(Varun) Adding extra discrete variable not connected to continuous
// variable throws segfault
// hfg.add(DecisionTreeFactor({m1, m2, "1 2 3 4"));
hfg.add(DecisionTreeFactor({m1, m2}, "1 2 3 4"));
HybridBayesTree::shared_ptr result = hfg.eliminateMultifrontal();
@ -176,7 +174,7 @@ TEST(HybridGaussianFactorGraph, Switching) {
// Ordering(KeyVector{X(1), X(4), X(2), X(6), X(9), X(8), X(3), X(7),
// X(5),
// M(1), M(4), M(2), M(6), M(8), M(3), M(7), M(5)});
KeyVector ordering;
Ordering ordering;
{
std::vector<int> naturalX(N);
@ -187,10 +185,6 @@ TEST(HybridGaussianFactorGraph, Switching) {
auto [ndX, lvls] = makeBinaryOrdering(ordX);
std::copy(ndX.begin(), ndX.end(), std::back_inserter(ordering));
// TODO(dellaert): this has no effect!
for (auto& l : lvls) {
l = -l;
}
}
{
std::vector<int> naturalC(N - 1);
@ -199,14 +193,11 @@ TEST(HybridGaussianFactorGraph, Switching) {
std::transform(naturalC.begin(), naturalC.end(), std::back_inserter(ordC),
[](int x) { return M(x); });
// std::copy(ordC.begin(), ordC.end(), std::back_inserter(ordering));
const auto [ndC, lvls] = makeBinaryOrdering(ordC);
std::copy(ndC.begin(), ndC.end(), std::back_inserter(ordering));
}
auto ordering_full = Ordering(ordering);
const auto [hbt, remaining] =
hfg->eliminatePartialMultifrontal(ordering_full);
const auto [hbt, remaining] = hfg->eliminatePartialMultifrontal(ordering);
// 12 cliques in the bayes tree and 0 remaining variables to eliminate.
EXPECT_LONGS_EQUAL(12, hbt->size());
@ -230,7 +221,7 @@ TEST(HybridGaussianFactorGraph, SwitchingISAM) {
// Ordering(KeyVector{X(1), X(4), X(2), X(6), X(9), X(8), X(3), X(7),
// X(5),
// M(1), M(4), M(2), M(6), M(8), M(3), M(7), M(5)});
KeyVector ordering;
Ordering ordering;
{
std::vector<int> naturalX(N);
@ -241,10 +232,6 @@ TEST(HybridGaussianFactorGraph, SwitchingISAM) {
auto [ndX, lvls] = makeBinaryOrdering(ordX);
std::copy(ndX.begin(), ndX.end(), std::back_inserter(ordering));
// TODO(dellaert): this has no effect!
for (auto& l : lvls) {
l = -l;
}
}
{
std::vector<int> naturalC(N - 1);
@ -257,10 +244,8 @@ TEST(HybridGaussianFactorGraph, SwitchingISAM) {
const auto [ndC, lvls] = makeBinaryOrdering(ordC);
std::copy(ndC.begin(), ndC.end(), std::back_inserter(ordering));
}
auto ordering_full = Ordering(ordering);
const auto [hbt, remaining] =
hfg->eliminatePartialMultifrontal(ordering_full);
const auto [hbt, remaining] = hfg->eliminatePartialMultifrontal(ordering);
auto new_fg = makeSwitchingChain(12);
auto isam = HybridGaussianISAM(*hbt);
@ -352,7 +337,7 @@ TEST(HybridBayesTree, OptimizeMultifrontal) {
Switching s(4);
HybridBayesTree::shared_ptr hybridBayesTree =
s.linearizedFactorGraph.eliminateMultifrontal();
s.linearizedFactorGraph().eliminateMultifrontal();
HybridValues delta = hybridBayesTree->optimize();
VectorValues expectedValues;
@ -364,30 +349,40 @@ TEST(HybridBayesTree, OptimizeMultifrontal) {
EXPECT(assert_equal(expectedValues, delta.continuous(), 1e-5));
}
namespace optimize_fixture {
HybridGaussianFactorGraph GetGaussianFactorGraph(size_t N) {
Switching s(N);
HybridGaussianFactorGraph graph;
for (size_t i = 0; i < N - 1; i++) {
graph.push_back(s.linearBinaryFactors.at(i));
}
for (size_t i = 0; i < N; i++) {
graph.push_back(s.linearUnaryFactors.at(i));
}
for (size_t i = 0; i < N - 1; i++) {
graph.push_back(s.modeChain.at(i));
}
return graph;
}
} // namespace optimize_fixture
/* ****************************************************************************/
// Test for optimizing a HybridBayesTree with a given assignment.
TEST(HybridBayesTree, OptimizeAssignment) {
Switching s(4);
using namespace optimize_fixture;
size_t N = 4;
HybridGaussianISAM isam;
HybridGaussianFactorGraph graph1;
// Add the 3 hybrid factors, x1-x2, x2-x3, x3-x4
for (size_t i = 1; i < 4; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the Gaussian factors, 1 prior on X(1),
// 3 measurements on X(2), X(3), X(4)
graph1.push_back(s.linearizedFactorGraph.at(0));
for (size_t i = 4; i <= 7; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the discrete factors
for (size_t i = 7; i <= 9; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
// Then add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
// Finally add the discrete factors
// m0, m1-m0, m2-m1
HybridGaussianFactorGraph graph1 = GetGaussianFactorGraph(N);
isam.update(graph1);
@ -409,12 +404,13 @@ TEST(HybridBayesTree, OptimizeAssignment) {
EXPECT(assert_equal(expected_delta, delta));
Switching s(N);
// Create ordering.
Ordering ordering;
for (size_t k = 0; k < s.K; k++) ordering.push_back(X(k));
const auto [hybridBayesNet, remainingFactorGraph] =
s.linearizedFactorGraph.eliminatePartialSequential(ordering);
s.linearizedFactorGraph().eliminatePartialSequential(ordering);
GaussianBayesNet gbn = hybridBayesNet->choose(assignment);
VectorValues expected = gbn.optimize();
@ -425,45 +421,31 @@ TEST(HybridBayesTree, OptimizeAssignment) {
/* ****************************************************************************/
// Test for optimizing a HybridBayesTree.
TEST(HybridBayesTree, Optimize) {
Switching s(4);
using namespace optimize_fixture;
size_t N = 4;
HybridGaussianISAM isam;
HybridGaussianFactorGraph graph1;
// Add the 3 hybrid factors, x1-x2, x2-x3, x3-x4
for (size_t i = 1; i < 4; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(2), X(3), X(4)
graph1.push_back(s.linearizedFactorGraph.at(0));
for (size_t i = 4; i <= 6; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the discrete factors
for (size_t i = 7; i <= 9; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
// Then add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
// Finally add the discrete factors
// m0, m1-m0, m2-m1
HybridGaussianFactorGraph graph1 = GetGaussianFactorGraph(N);
isam.update(graph1);
HybridValues delta = isam.optimize();
Switching s(N);
// Create ordering.
Ordering ordering;
for (size_t k = 0; k < s.K; k++) ordering.push_back(X(k));
const auto [hybridBayesNet, remainingFactorGraph] =
s.linearizedFactorGraph.eliminatePartialSequential(ordering);
s.linearizedFactorGraph().eliminatePartialSequential(ordering);
DiscreteFactorGraph dfg;
for (auto&& f : *remainingFactorGraph) {
auto discreteFactor = dynamic_pointer_cast<DiscreteFactor>(f);
assert(discreteFactor);
dfg.push_back(discreteFactor);
}
DiscreteFactorGraph dfg = remainingFactorGraph->discreteFactors();
// Add the probabilities for each branch
DiscreteKeys discrete_keys = {{M(0), 2}, {M(1), 2}, {M(2), 2}};
@ -481,27 +463,18 @@ TEST(HybridBayesTree, Optimize) {
/* ****************************************************************************/
// Test for choosing a GaussianBayesTree from a HybridBayesTree.
TEST(HybridBayesTree, Choose) {
Switching s(4);
using namespace optimize_fixture;
size_t N = 4;
HybridGaussianISAM isam;
HybridGaussianFactorGraph graph1;
// Add the 3 hybrid factors, x1-x2, x2-x3, x3-x4
for (size_t i = 1; i < 4; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(2), X(3), X(4)
graph1.push_back(s.linearizedFactorGraph.at(0));
for (size_t i = 4; i <= 6; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the discrete factors
for (size_t i = 7; i <= 9; i++) {
graph1.push_back(s.linearizedFactorGraph.at(i));
}
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
// Then add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
// Finally add the discrete factors
// m0, m1-m0, m2-m1
HybridGaussianFactorGraph graph1 = GetGaussianFactorGraph(N);
isam.update(graph1);
@ -513,8 +486,9 @@ TEST(HybridBayesTree, Choose) {
GaussianBayesTree gbt = isam.choose(assignment);
// Specify ordering so it matches that of HybridGaussianISAM.
Switching s(N);
Ordering ordering(KeyVector{X(0), X(1), X(2), X(3), M(0), M(1), M(2)});
auto bayesTree = s.linearizedFactorGraph.eliminateMultifrontal(ordering);
auto bayesTree = s.linearizedFactorGraph().eliminateMultifrontal(ordering);
auto expected_gbt = bayesTree->choose(assignment);

6
gtsam/hybrid/tests/testHybridEstimation.cpp
View File

@ -82,7 +82,7 @@ TEST(HybridEstimation, Full) {
// Switching example of robot moving in 1D
// with given measurements and equal mode priors.
Switching switching(K, 1.0, 0.1, measurements, "1/1 1/1");
HybridGaussianFactorGraph graph = switching.linearizedFactorGraph;
HybridGaussianFactorGraph graph = switching.linearizedFactorGraph();
Ordering hybridOrdering;
for (size_t k = 0; k < K; k++) {
@ -325,7 +325,7 @@ TEST(HybridEstimation, Probability) {
// given measurements and equal mode priors.
Switching switching(K, between_sigma, measurement_sigma, measurements,
"1/1 1/1");
auto graph = switching.linearizedFactorGraph;
auto graph = switching.linearizedFactorGraph();
// Continuous elimination
Ordering continuous_ordering(graph.continuousKeySet());
@ -365,7 +365,7 @@ TEST(HybridEstimation, ProbabilityMultifrontal) {
// mode priors.
Switching switching(K, between_sigma, measurement_sigma, measurements,
"1/1 1/1");
auto graph = switching.linearizedFactorGraph;
auto graph = switching.linearizedFactorGraph();
// Get the tree of unnormalized probabilities for each mode sequence.
AlgebraicDecisionTree<Key> expected_probPrimeTree = GetProbPrimeTree(graph);

8
gtsam/hybrid/tests/testHybridGaussianConditional.cpp
View File

@ -275,6 +275,11 @@ TEST(HybridGaussianConditional, Prune) {
// Check that the pruned HybridGaussianConditional has 2 conditionals
EXPECT_LONGS_EQUAL(2, pruned->nrComponents());
// Check that the minimum negLogConstant is set correctly
EXPECT_DOUBLES_EQUAL(
hgc.conditionals()({{M(1), 0}, {M(2), 1}})->negLogConstant(),
pruned->negLogConstant(), 1e-9);
}
{
const std::vector<double> potentials{0.2, 0, 0.3, 0, //
@ -285,6 +290,9 @@ TEST(HybridGaussianConditional, Prune) {
// Check that the pruned HybridGaussianConditional has 3 conditionals
EXPECT_LONGS_EQUAL(3, pruned->nrComponents());
// Check that the minimum negLogConstant is correct
EXPECT_DOUBLES_EQUAL(hgc.negLogConstant(), pruned->negLogConstant(), 1e-9);
}
}

158
gtsam/hybrid/tests/testHybridGaussianFactor.cpp
View File

@ -194,164 +194,6 @@ TEST(HybridGaussianFactor, Error) {
4.0, hybridFactor.error({continuousValues, discreteValues}), 1e-9);
}
/* ************************************************************************* */
namespace test_direct_factor_graph {
/**
* @brief Create a Factor Graph by directly specifying all
* the factors instead of creating conditionals first.
* This way we can directly provide the likelihoods and
* then perform linearization.
*
* @param values Initial values to linearize around.
* @param means The means of the HybridGaussianFactor components.
* @param sigmas The covariances of the HybridGaussianFactor components.
* @param m1 The discrete key.
* @return HybridGaussianFactorGraph
*/
static HybridGaussianFactorGraph CreateFactorGraph(
const gtsam::Values &values, const std::vector<double> &means,
const std::vector<double> &sigmas, DiscreteKey &m1,
double measurement_noise = 1e-3) {
auto model0 = noiseModel::Isotropic::Sigma(1, sigmas[0]);
auto model1 = noiseModel::Isotropic::Sigma(1, sigmas[1]);
auto prior_noise = noiseModel::Isotropic::Sigma(1, measurement_noise);
auto f0 =
std::make_shared<BetweenFactor<double>>(X(0), X(1), means[0], model0)
->linearize(values);
auto f1 =
std::make_shared<BetweenFactor<double>>(X(0), X(1), means[1], model1)
->linearize(values);
// Create HybridGaussianFactor
// We take negative since we want
// the underlying scalar to be log(\sqrt(|2πΣ|))
std::vector<GaussianFactorValuePair> factors{{f0, model0->negLogConstant()},
{f1, model1->negLogConstant()}};
HybridGaussianFactor motionFactor(m1, factors);
HybridGaussianFactorGraph hfg;
hfg.push_back(motionFactor);
hfg.push_back(PriorFactor<double>(X(0), values.at<double>(X(0)), prior_noise)
.linearize(values));
return hfg;
}
} // namespace test_direct_factor_graph
/* ************************************************************************* */
/**
* @brief Test components with differing means but the same covariances.
* The factor graph is
* *-X1-*-X2
* |
* M1
*/
TEST(HybridGaussianFactor, DifferentMeansFG) {
using namespace test_direct_factor_graph;
DiscreteKey m1(M(1), 2);
Values values;
double x1 = 0.0, x2 = 1.75;
values.insert(X(0), x1);
values.insert(X(1), x2);
std::vector<double> means = {0.0, 2.0}, sigmas = {1e-0, 1e-0};
HybridGaussianFactorGraph hfg = CreateFactorGraph(values, means, sigmas, m1);
{
auto bn = hfg.eliminateSequential();
HybridValues actual = bn->optimize();
HybridValues expected(
VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(-1.75)}},
DiscreteValues{{M(1), 0}});
EXPECT(assert_equal(expected, actual));
DiscreteValues dv0{{M(1), 0}};
VectorValues cont0 = bn->optimize(dv0);
double error0 = bn->error(HybridValues(cont0, dv0));
// regression
EXPECT_DOUBLES_EQUAL(0.69314718056, error0, 1e-9);
DiscreteValues dv1{{M(1), 1}};
VectorValues cont1 = bn->optimize(dv1);
double error1 = bn->error(HybridValues(cont1, dv1));
EXPECT_DOUBLES_EQUAL(error0, error1, 1e-9);
}
{
auto prior_noise = noiseModel::Isotropic::Sigma(1, 1e-3);
hfg.push_back(
PriorFactor<double>(X(1), means[1], prior_noise).linearize(values));
auto bn = hfg.eliminateSequential();
HybridValues actual = bn->optimize();
HybridValues expected(
VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(0.25)}},
DiscreteValues{{M(1), 1}});
EXPECT(assert_equal(expected, actual));
{
DiscreteValues dv{{M(1), 0}};
VectorValues cont = bn->optimize(dv);
double error = bn->error(HybridValues(cont, dv));
// regression
EXPECT_DOUBLES_EQUAL(2.12692448787, error, 1e-9);
}
{
DiscreteValues dv{{M(1), 1}};
VectorValues cont = bn->optimize(dv);
double error = bn->error(HybridValues(cont, dv));
// regression
EXPECT_DOUBLES_EQUAL(0.126928487854, error, 1e-9);
}
}
}
/* ************************************************************************* */
/**
* @brief Test components with differing covariances but the same means.
* The factor graph is
* *-X1-*-X2
* |
* M1
*/
TEST(HybridGaussianFactor, DifferentCovariancesFG) {
using namespace test_direct_factor_graph;
DiscreteKey m1(M(1), 2);
Values values;
double x1 = 1.0, x2 = 1.0;
values.insert(X(0), x1);
values.insert(X(1), x2);
std::vector<double> means = {0.0, 0.0}, sigmas = {1e2, 1e-2};
// Create FG with HybridGaussianFactor and prior on X1
HybridGaussianFactorGraph fg = CreateFactorGraph(values, means, sigmas, m1);
auto hbn = fg.eliminateSequential();
VectorValues cv;
cv.insert(X(0), Vector1(0.0));
cv.insert(X(1), Vector1(0.0));
DiscreteValues dv0{{M(1), 0}};
DiscreteValues dv1{{M(1), 1}};
DiscreteConditional expected_m1(m1, "0.5/0.5");
DiscreteConditional actual_m1 = *(hbn->at(2)->asDiscrete());
EXPECT(assert_equal(expected_m1, actual_m1));
}
/* ************************************************************************* */
int main() {
TestResult tr;

58
gtsam/hybrid/tests/testHybridGaussianFactorGraph.cpp
View File

@ -175,7 +175,7 @@ TEST(HybridBayesNet, Switching) {
Switching s(2, betweenSigma, priorSigma);
// Check size of linearized factor graph
const HybridGaussianFactorGraph &graph = s.linearizedFactorGraph;
const HybridGaussianFactorGraph &graph = s.linearizedFactorGraph();
EXPECT_LONGS_EQUAL(4, graph.size());
// Create some continuous and discrete values
@ -184,7 +184,7 @@ TEST(HybridBayesNet, Switching) {
const DiscreteValues modeZero{{M(0), 0}}, modeOne{{M(0), 1}};
// Get the hybrid gaussian factor and check it is as expected
auto hgf = std::dynamic_pointer_cast<HybridGaussianFactor>(graph.at(1));
auto hgf = std::dynamic_pointer_cast<HybridGaussianFactor>(graph.at(2));
CHECK(hgf);
// Get factors and scalars for both modes
@ -298,7 +298,7 @@ TEST(HybridBayesNet, Switching) {
factors_x1.push_back(
factor); // Use the remaining factor from previous elimination
factors_x1.push_back(
graph.at(2)); // Add the factor for x1 from the original graph
graph.at(1)); // Add the factor for x1 from the original graph
// Test collectProductFactor for x1 clique
auto productFactor_x1 = factors_x1.collectProductFactor();
@ -356,7 +356,7 @@ TEST(HybridGaussianFactorGraph, ErrorAndProbPrime) {
Switching s(3);
// Check size of linearized factor graph
const HybridGaussianFactorGraph &graph = s.linearizedFactorGraph;
const HybridGaussianFactorGraph &graph = s.linearizedFactorGraph();
EXPECT_LONGS_EQUAL(7, graph.size());
// Eliminate the graph
@ -383,16 +383,16 @@ TEST(HybridGaussianFactorGraph, ErrorAndProbPrime) {
TEST(HybridGaussianFactorGraph, DiscreteSelection) {
Switching s(3);
HybridGaussianFactorGraph graph = s.linearizedFactorGraph;
HybridGaussianFactorGraph graph = s.linearizedFactorGraph();
DiscreteValues dv00{{M(0), 0}, {M(1), 0}};
GaussianFactorGraph continuous_00 = graph(dv00);
GaussianFactorGraph expected_00;
expected_00.push_back(JacobianFactor(X(0), I_1x1 * 10, Vector1(-10)));
expected_00.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-1)));
expected_00.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-1)));
expected_00.push_back(JacobianFactor(X(1), I_1x1 * 10, Vector1(-10)));
expected_00.push_back(JacobianFactor(X(2), I_1x1 * 10, Vector1(-10)));
expected_00.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-1)));
expected_00.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-1)));
EXPECT(assert_equal(expected_00, continuous_00));
@ -400,10 +400,10 @@ TEST(HybridGaussianFactorGraph, DiscreteSelection) {
GaussianFactorGraph continuous_01 = graph(dv01);
GaussianFactorGraph expected_01;
expected_01.push_back(JacobianFactor(X(0), I_1x1 * 10, Vector1(-10)));
expected_01.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-1)));
expected_01.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-0)));
expected_01.push_back(JacobianFactor(X(1), I_1x1 * 10, Vector1(-10)));
expected_01.push_back(JacobianFactor(X(2), I_1x1 * 10, Vector1(-10)));
expected_01.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-1)));
expected_01.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-0)));
EXPECT(assert_equal(expected_01, continuous_01));
@ -411,10 +411,10 @@ TEST(HybridGaussianFactorGraph, DiscreteSelection) {
GaussianFactorGraph continuous_10 = graph(dv10);
GaussianFactorGraph expected_10;
expected_10.push_back(JacobianFactor(X(0), I_1x1 * 10, Vector1(-10)));
expected_10.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-0)));
expected_10.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-1)));
expected_10.push_back(JacobianFactor(X(1), I_1x1 * 10, Vector1(-10)));
expected_10.push_back(JacobianFactor(X(2), I_1x1 * 10, Vector1(-10)));
expected_10.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-0)));
expected_10.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-1)));
EXPECT(assert_equal(expected_10, continuous_10));
@ -422,16 +422,16 @@ TEST(HybridGaussianFactorGraph, DiscreteSelection) {
GaussianFactorGraph continuous_11 = graph(dv11);
GaussianFactorGraph expected_11;
expected_11.push_back(JacobianFactor(X(0), I_1x1 * 10, Vector1(-10)));
expected_11.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-0)));
expected_11.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-0)));
expected_11.push_back(JacobianFactor(X(1), I_1x1 * 10, Vector1(-10)));
expected_11.push_back(JacobianFactor(X(2), I_1x1 * 10, Vector1(-10)));
expected_11.push_back(JacobianFactor(X(0), -I_1x1, X(1), I_1x1, Vector1(-0)));
expected_11.push_back(JacobianFactor(X(1), -I_1x1, X(2), I_1x1, Vector1(-0)));
EXPECT(assert_equal(expected_11, continuous_11));
}
/* ************************************************************************* */
TEST(HybridGaussianFactorGraph, optimize) {
TEST(HybridGaussianFactorGraph, Optimize) {
HybridGaussianFactorGraph hfg;
hfg.add(JacobianFactor(X(0), I_3x3, Z_3x1));
@ -451,16 +451,16 @@ TEST(HybridGaussianFactorGraph, Conditionals) {
Switching switching(4);
HybridGaussianFactorGraph hfg;
hfg.push_back(switching.linearizedFactorGraph.at(0)); // P(X0)
hfg.push_back(switching.linearUnaryFactors.at(0)); // P(X0)
Ordering ordering;
ordering.push_back(X(0));
HybridBayesNet::shared_ptr bayes_net = hfg.eliminateSequential(ordering);
HybridGaussianFactorGraph hfg2;
hfg2.push_back(*bayes_net); // P(X0)
hfg2.push_back(switching.linearizedFactorGraph.at(1)); // P(X0, X1 | M0)
hfg2.push_back(switching.linearizedFactorGraph.at(2)); // P(X1, X2 | M1)
hfg2.push_back(switching.linearizedFactorGraph.at(5)); // P(M1)
hfg2.push_back(*bayes_net); // P(X0)
hfg2.push_back(switching.linearBinaryFactors.at(0)); // P(X0, X1 | M0)
hfg2.push_back(switching.linearBinaryFactors.at(1)); // P(X1, X2 | M1)
hfg2.push_back(switching.linearUnaryFactors.at(2)); // P(X2)
ordering += X(1), X(2), M(0), M(1);
// Created product of first two factors and check eliminate:
@ -510,13 +510,13 @@ TEST(HybridGaussianFactorGraph, IncrementalErrorTree) {
Switching s(4);
HybridGaussianFactorGraph graph;
graph.push_back(s.linearizedFactorGraph.at(0)); // f(X0)
graph.push_back(s.linearizedFactorGraph.at(1)); // f(X0, X1, M0)
graph.push_back(s.linearizedFactorGraph.at(2)); // f(X1, X2, M1)
graph.push_back(s.linearizedFactorGraph.at(4)); // f(X1)
graph.push_back(s.linearizedFactorGraph.at(5)); // f(X2)
graph.push_back(s.linearizedFactorGraph.at(7)); // f(M0)
graph.push_back(s.linearizedFactorGraph.at(8)); // f(M0, M1)
graph.push_back(s.linearUnaryFactors.at(0)); // f(X0)
graph.push_back(s.linearBinaryFactors.at(0)); // f(X0, X1, M0)
graph.push_back(s.linearBinaryFactors.at(1)); // f(X1, X2, M1)
graph.push_back(s.linearUnaryFactors.at(1)); // f(X1)
graph.push_back(s.linearUnaryFactors.at(2)); // f(X2)
graph.push_back(s.modeChain.at(0)); // f(M0)
graph.push_back(s.modeChain.at(1)); // f(M0, M1)
HybridBayesNet::shared_ptr hybridBayesNet = graph.eliminateSequential();
EXPECT_LONGS_EQUAL(5, hybridBayesNet->size());
@ -531,8 +531,8 @@ TEST(HybridGaussianFactorGraph, IncrementalErrorTree) {
graph = HybridGaussianFactorGraph();
graph.push_back(*hybridBayesNet);
graph.push_back(s.linearizedFactorGraph.at(3)); // f(X2, X3, M2)
graph.push_back(s.linearizedFactorGraph.at(6)); // f(X3)
graph.push_back(s.linearBinaryFactors.at(2)); // f(X2, X3, M2)
graph.push_back(s.linearUnaryFactors.at(3)); // f(X3)
hybridBayesNet = graph.eliminateSequential();
EXPECT_LONGS_EQUAL(7, hybridBayesNet->size());
@ -545,7 +545,7 @@ TEST(HybridGaussianFactorGraph, IncrementalErrorTree) {
/* ****************************************************************************/
// Check that collectProductFactor works correctly.
TEST(HybridGaussianFactorGraph, collectProductFactor) {
TEST(HybridGaussianFactorGraph, CollectProductFactor) {
const int num_measurements = 1;
VectorValues vv{{Z(0), Vector1(5.0)}};
auto fg = tiny::createHybridGaussianFactorGraph(num_measurements, vv);

63
gtsam/hybrid/tests/testHybridGaussianISAM.cpp
View File

@ -42,21 +42,21 @@ using symbol_shorthand::Z;
/* ****************************************************************************/
namespace switching3 {
// ϕ(x0) ϕ(x0,x1,m0) ϕ(x1,x2,m1) ϕ(x1;z1) ϕ(x2;z2) ϕ(m0) ϕ(m0,m1)
// ϕ(x0) ϕ(x1;z1) ϕ(x2;z2) ϕ(x0,x1,m0) ϕ(x1,x2,m1) ϕ(m0) ϕ(m0,m1)
const Switching switching(3);
const HybridGaussianFactorGraph &lfg = switching.linearizedFactorGraph;
const HybridGaussianFactorGraph &lfg = switching.linearizedFactorGraph();
// First update graph: ϕ(x0) ϕ(x0,x1,m0) ϕ(m0)
const HybridGaussianFactorGraph graph1{lfg.at(0), lfg.at(1), lfg.at(5)};
const HybridGaussianFactorGraph graph1{lfg.at(0), lfg.at(3), lfg.at(5)};
// Second update graph: ϕ(x1,x2,m1) ϕ(x1;z1) ϕ(x2;z2) ϕ(m0,m1)
const HybridGaussianFactorGraph graph2{lfg.at(2), lfg.at(3), lfg.at(4),
const HybridGaussianFactorGraph graph2{lfg.at(4), lfg.at(1), lfg.at(2),
lfg.at(6)};
} // namespace switching3
/* ****************************************************************************/
// Test if we can perform elimination incrementally.
TEST(HybridGaussianElimination, IncrementalElimination) {
TEST(HybridGaussianISAM, IncrementalElimination) {
using namespace switching3;
HybridGaussianISAM isam;
@ -88,7 +88,7 @@ TEST(HybridGaussianElimination, IncrementalElimination) {
/* ****************************************************************************/
// Test if we can incrementally do the inference
TEST(HybridGaussianElimination, IncrementalInference) {
TEST(HybridGaussianISAM, IncrementalInference) {
using namespace switching3;
HybridGaussianISAM isam;
@ -108,7 +108,7 @@ TEST(HybridGaussianElimination, IncrementalInference) {
// Now we calculate the expected factors using full elimination
const auto [expectedHybridBayesTree, expectedRemainingGraph] =
switching.linearizedFactorGraph.eliminatePartialMultifrontal(ordering);
switching.linearizedFactorGraph().eliminatePartialMultifrontal(ordering);
// The densities on X(0) should be the same
auto x0_conditional = dynamic_pointer_cast<HybridGaussianConditional>(
@ -156,21 +156,20 @@ TEST(HybridGaussianElimination, IncrementalInference) {
/* ****************************************************************************/
// Test if we can approximately do the inference
TEST(HybridGaussianElimination, Approx_inference) {
TEST(HybridGaussianISAM, ApproxInference) {
Switching switching(4);
HybridGaussianISAM incrementalHybrid;
HybridGaussianFactorGraph graph1;
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
for (size_t i = 1; i < 4; i++) {
graph1.push_back(switching.linearizedFactorGraph.at(i));
for (size_t i = 0; i < 3; i++) {
graph1.push_back(switching.linearBinaryFactors.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
graph1.push_back(switching.linearizedFactorGraph.at(0));
for (size_t i = 4; i <= 7; i++) {
graph1.push_back(switching.linearizedFactorGraph.at(i));
// Add the Gaussian factors, 1 prior on x0,
// 3 measurements on x1, x2, x3
for (size_t i = 0; i <= 3; i++) {
graph1.push_back(switching.linearUnaryFactors.at(i));
}
// Create ordering.
@ -181,7 +180,7 @@ TEST(HybridGaussianElimination, Approx_inference) {
// Now we calculate the actual factors using full elimination
const auto [unPrunedHybridBayesTree, unPrunedRemainingGraph] =
switching.linearizedFactorGraph.eliminatePartialMultifrontal(ordering);
switching.linearizedFactorGraph().eliminatePartialMultifrontal(ordering);
size_t maxNrLeaves = 5;
incrementalHybrid.update(graph1);
@ -259,28 +258,26 @@ TEST(HybridGaussianElimination, Approx_inference) {
/* ****************************************************************************/
// Test approximate inference with an additional pruning step.
TEST(HybridGaussianElimination, IncrementalApproximate) {
TEST(HybridGaussianISAM, IncrementalApproximate) {
Switching switching(5);
HybridGaussianISAM incrementalHybrid;
HybridGaussianFactorGraph graph1;
HybridGaussianFactorGraph graph;
/***** Run Round 1 *****/
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
for (size_t i = 1; i < 4; i++) {
graph1.push_back(switching.linearizedFactorGraph.at(i));
for (size_t i = 0; i < 3; i++) {
graph.push_back(switching.linearBinaryFactors.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
graph1.push_back(switching.linearizedFactorGraph.at(0));
for (size_t i = 5; i <= 7; i++) {
graph1.push_back(switching.linearizedFactorGraph.at(i));
// Add the Gaussian factors, 1 prior on x0,
// 3 measurements on x1, x2, x3
for (size_t i = 0; i <= 3; i++) {
graph.push_back(switching.linearUnaryFactors.at(i));
}
// Run update with pruning
size_t maxComponents = 5;
incrementalHybrid.update(graph1);
incrementalHybrid.prune(maxComponents);
incrementalHybrid.update(graph, maxComponents);
// Check if we have a bayes tree with 4 hybrid nodes,
// each with 2, 4, 8, and 5 (pruned) leaves respectively.
@ -295,13 +292,12 @@ TEST(HybridGaussianElimination, IncrementalApproximate) {
5, incrementalHybrid[X(3)]->conditional()->asHybrid()->nrComponents());
/***** Run Round 2 *****/
HybridGaussianFactorGraph graph2;
graph2.push_back(switching.linearizedFactorGraph.at(4));
graph2.push_back(switching.linearizedFactorGraph.at(8));
graph = HybridGaussianFactorGraph();
graph.push_back(switching.linearBinaryFactors.at(3)); // hybrid x3-x4
graph.push_back(switching.linearUnaryFactors.at(4)); // x4
// Run update with pruning a second time.
incrementalHybrid.update(graph2);
incrementalHybrid.prune(maxComponents);
incrementalHybrid.update(graph, maxComponents);
// Check if we have a bayes tree with pruned hybrid nodes,
// with 5 (pruned) leaves.
@ -472,8 +468,7 @@ TEST(HybridGaussianISAM, NonTrivial) {
fg = HybridNonlinearFactorGraph();
// Keep pruning!
inc.update(gfg);
inc.prune(3);
inc.update(gfg, 3);
// The final discrete graph should not be empty since we have eliminated
// all continuous variables.

2
gtsam/hybrid/tests/testHybridGaussianProductFactor.cpp
View File

@ -189,8 +189,10 @@ TEST(HybridGaussianProductFactor, AddPruned) {
product += prunedFactorB;
EXPECT_LONGS_EQUAL(6, product.nrLeaves());
#ifdef GTSAM_DT_MERGING
auto pruned = product.removeEmpty();
EXPECT_LONGS_EQUAL(5, pruned.nrLeaves());
#endif
}
/* ************************************************************************* */

170
gtsam/hybrid/tests/testHybridMotionModel.cpp
View File

@ -124,7 +124,7 @@ std::pair<double, double> approximateDiscreteMarginal(
* the posterior probability of m1 should be 0.5/0.5.
* Getting a measurement on z1 gives use more information.
*/
TEST(HybridGaussianFactor, TwoStateModel) {
TEST(HybridGaussianFactorGraph, TwoStateModel) {
double mu0 = 1.0, mu1 = 3.0;
double sigma = 0.5;
auto hybridMotionModel = CreateHybridMotionModel(mu0, mu1, sigma, sigma);
@ -178,7 +178,7 @@ TEST(HybridGaussianFactor, TwoStateModel) {
* the P(m1) should be 0.5/0.5.
* Getting a measurement on z1 gives use more information.
*/
TEST(HybridGaussianFactor, TwoStateModel2) {
TEST(HybridGaussianFactorGraph, TwoStateModel2) {
double mu0 = 1.0, mu1 = 3.0;
double sigma0 = 0.5, sigma1 = 2.0;
auto hybridMotionModel = CreateHybridMotionModel(mu0, mu1, sigma0, sigma1);
@ -198,7 +198,7 @@ TEST(HybridGaussianFactor, TwoStateModel2) {
{VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(1.0)}},
VectorValues{{X(0), Vector1(0.5)}, {X(1), Vector1(3.0)}}}) {
vv.insert(given); // add measurements for HBN
const auto& expectedDiscretePosterior = hbn.discretePosterior(vv);
const auto &expectedDiscretePosterior = hbn.discretePosterior(vv);
// Equality of posteriors asserts that the factor graph is correct (same
// ratios for all modes)
@ -234,7 +234,7 @@ TEST(HybridGaussianFactor, TwoStateModel2) {
{VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(1.0)}},
VectorValues{{X(0), Vector1(0.5)}, {X(1), Vector1(3.0)}}}) {
vv.insert(given); // add measurements for HBN
const auto& expectedDiscretePosterior = hbn.discretePosterior(vv);
const auto &expectedDiscretePosterior = hbn.discretePosterior(vv);
// Equality of posteriors asserts that the factor graph is correct (same
// ratios for all modes)
@ -281,7 +281,7 @@ TEST(HybridGaussianFactor, TwoStateModel2) {
* the p(m1) should be 0.5/0.5.
* Getting a measurement on z1 gives use more information.
*/
TEST(HybridGaussianFactor, TwoStateModel3) {
TEST(HybridGaussianFactorGraph, TwoStateModel3) {
double mu = 1.0;
double sigma0 = 0.5, sigma1 = 2.0;
auto hybridMotionModel = CreateHybridMotionModel(mu, mu, sigma0, sigma1);
@ -366,7 +366,7 @@ TEST(HybridGaussianFactor, TwoStateModel3) {
* measurements and vastly different motion model: either stand still or move
* far. This yields a very informative posterior.
*/
TEST(HybridGaussianFactor, TwoStateModel4) {
TEST(HybridGaussianFactorGraph, TwoStateModel4) {
double mu0 = 0.0, mu1 = 10.0;
double sigma0 = 0.2, sigma1 = 5.0;
auto hybridMotionModel = CreateHybridMotionModel(mu0, mu1, sigma0, sigma1);
@ -385,6 +385,164 @@ TEST(HybridGaussianFactor, TwoStateModel4) {
EXPECT(assert_equal(expected, *(bn->at(2)->asDiscrete()), 0.002));
}
/* ************************************************************************* */
namespace test_direct_factor_graph {
/**
* @brief Create a Factor Graph by directly specifying all
* the factors instead of creating conditionals first.
* This way we can directly provide the likelihoods and
* then perform linearization.
*
* @param values Initial values to linearize around.
* @param means The means of the HybridGaussianFactor components.
* @param sigmas The covariances of the HybridGaussianFactor components.
* @param m1 The discrete key.
* @return HybridGaussianFactorGraph
*/
static HybridGaussianFactorGraph CreateFactorGraph(
const gtsam::Values &values, const std::vector<double> &means,
const std::vector<double> &sigmas, DiscreteKey &m1,
double measurement_noise = 1e-3) {
auto model0 = noiseModel::Isotropic::Sigma(1, sigmas[0]);
auto model1 = noiseModel::Isotropic::Sigma(1, sigmas[1]);
auto prior_noise = noiseModel::Isotropic::Sigma(1, measurement_noise);
auto f0 =
std::make_shared<BetweenFactor<double>>(X(0), X(1), means[0], model0)
->linearize(values);
auto f1 =
std::make_shared<BetweenFactor<double>>(X(0), X(1), means[1], model1)
->linearize(values);
// Create HybridGaussianFactor
// We take negative since we want
// the underlying scalar to be log(\sqrt(|2πΣ|))
std::vector<GaussianFactorValuePair> factors{{f0, model0->negLogConstant()},
{f1, model1->negLogConstant()}};
HybridGaussianFactor motionFactor(m1, factors);
HybridGaussianFactorGraph hfg;
hfg.push_back(motionFactor);
hfg.push_back(PriorFactor<double>(X(0), values.at<double>(X(0)), prior_noise)
.linearize(values));
return hfg;
}
} // namespace test_direct_factor_graph
/* ************************************************************************* */
/**
* @brief Test components with differing means but the same covariances.
* The factor graph is
* *-X1-*-X2
* |
* M1
*/
TEST(HybridGaussianFactorGraph, DifferentMeans) {
using namespace test_direct_factor_graph;
DiscreteKey m1(M(1), 2);
Values values;
double x1 = 0.0, x2 = 1.75;
values.insert(X(0), x1);
values.insert(X(1), x2);
std::vector<double> means = {0.0, 2.0}, sigmas = {1e-0, 1e-0};
HybridGaussianFactorGraph hfg = CreateFactorGraph(values, means, sigmas, m1);
{
auto bn = hfg.eliminateSequential();
HybridValues actual = bn->optimize();
HybridValues expected(
VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(-1.75)}},
DiscreteValues{{M(1), 0}});
EXPECT(assert_equal(expected, actual));
DiscreteValues dv0{{M(1), 0}};
VectorValues cont0 = bn->optimize(dv0);
double error0 = bn->error(HybridValues(cont0, dv0));
// regression
EXPECT_DOUBLES_EQUAL(0.69314718056, error0, 1e-9);
DiscreteValues dv1{{M(1), 1}};
VectorValues cont1 = bn->optimize(dv1);
double error1 = bn->error(HybridValues(cont1, dv1));
EXPECT_DOUBLES_EQUAL(error0, error1, 1e-9);
}
{
auto prior_noise = noiseModel::Isotropic::Sigma(1, 1e-3);
hfg.push_back(
PriorFactor<double>(X(1), means[1], prior_noise).linearize(values));
auto bn = hfg.eliminateSequential();
HybridValues actual = bn->optimize();
HybridValues expected(
VectorValues{{X(0), Vector1(0.0)}, {X(1), Vector1(0.25)}},
DiscreteValues{{M(1), 1}});
EXPECT(assert_equal(expected, actual));
{
DiscreteValues dv{{M(1), 0}};
VectorValues cont = bn->optimize(dv);
double error = bn->error(HybridValues(cont, dv));
// regression
EXPECT_DOUBLES_EQUAL(2.12692448787, error, 1e-9);
}
{
DiscreteValues dv{{M(1), 1}};
VectorValues cont = bn->optimize(dv);
double error = bn->error(HybridValues(cont, dv));
// regression
EXPECT_DOUBLES_EQUAL(0.126928487854, error, 1e-9);
}
}
}
/* ************************************************************************* */
/**
* @brief Test components with differing covariances but the same means.
* The factor graph is
* *-X1-*-X2
* |
* M1
*/
TEST(HybridGaussianFactorGraph, DifferentCovariances) {
using namespace test_direct_factor_graph;
DiscreteKey m1(M(1), 2);
Values values;
double x1 = 1.0, x2 = 1.0;
values.insert(X(0), x1);
values.insert(X(1), x2);
std::vector<double> means = {0.0, 0.0}, sigmas = {1e2, 1e-2};
// Create FG with HybridGaussianFactor and prior on X1
HybridGaussianFactorGraph fg = CreateFactorGraph(values, means, sigmas, m1);
auto hbn = fg.eliminateSequential();
VectorValues cv;
cv.insert(X(0), Vector1(0.0));
cv.insert(X(1), Vector1(0.0));
DiscreteValues dv0{{M(1), 0}};
DiscreteValues dv1{{M(1), 1}};
DiscreteConditional expected_m1(m1, "0.5/0.5");
DiscreteConditional actual_m1 = *(hbn->at(2)->asDiscrete());
EXPECT(assert_equal(expected_m1, actual_m1));
}
/* ************************************************************************* */
int main() {
TestResult tr;

150
gtsam/hybrid/tests/testHybridNonlinearFactorGraph.cpp
View File

@ -249,7 +249,7 @@ TEST(HybridNonlinearFactorGraph, Switching) {
Switching self(3);
EXPECT_LONGS_EQUAL(7, self.nonlinearFactorGraph().size());
EXPECT_LONGS_EQUAL(7, self.linearizedFactorGraph.size());
EXPECT_LONGS_EQUAL(7, self.linearizedFactorGraph().size());
}
/****************************************************************************
@ -276,7 +276,7 @@ TEST(HybridNonlinearFactorGraph, EliminationTree) {
for (size_t k = 0; k < self.K; k++) ordering.push_back(X(k));
// Create elimination tree.
HybridEliminationTree etree(self.linearizedFactorGraph, ordering);
HybridEliminationTree etree(self.linearizedFactorGraph(), ordering);
EXPECT_LONGS_EQUAL(1, etree.roots().size())
}
@ -286,12 +286,12 @@ TEST(HybridNonlinearFactorGraph, EliminationTree) {
TEST(GaussianElimination, Eliminate_x0) {
Switching self(3);
// Gather factors on x1, has a simple Gaussian and a hybrid factor.
// Gather factors on x0, has a simple Gaussian and a hybrid factor.
HybridGaussianFactorGraph factors;
// Add gaussian prior
factors.push_back(self.linearizedFactorGraph[0]);
factors.push_back(self.linearUnaryFactors[0]);
// Add first hybrid factor
factors.push_back(self.linearizedFactorGraph[1]);
factors.push_back(self.linearBinaryFactors[0]);
// Eliminate x0
const Ordering ordering{X(0)};
@ -313,8 +313,8 @@ TEST(HybridsGaussianElimination, Eliminate_x1) {
// Gather factors on x1, will be two hybrid factors (with x0 and x2, resp.).
HybridGaussianFactorGraph factors;
factors.push_back(self.linearizedFactorGraph[1]); // involves m0
factors.push_back(self.linearizedFactorGraph[2]); // involves m1
factors.push_back(self.linearBinaryFactors[0]); // involves m0
factors.push_back(self.linearBinaryFactors[1]); // involves m1
// Eliminate x1
const Ordering ordering{X(1)};
@ -349,7 +349,7 @@ GaussianFactorGraph::shared_ptr batchGFG(double between,
TEST(HybridGaussianElimination, EliminateHybrid_2_Variable) {
Switching self(2, 1.0, 0.1);
auto factors = self.linearizedFactorGraph;
auto factors = self.linearizedFactorGraph();
// Eliminate x0
const Ordering ordering{X(0), X(1)};
@ -380,15 +380,13 @@ TEST(HybridGaussianElimination, EliminateHybrid_2_Variable) {
TEST(HybridNonlinearFactorGraph, Partial_Elimination) {
Switching self(3);
auto linearizedFactorGraph = self.linearizedFactorGraph;
// Create ordering of only continuous variables.
Ordering ordering;
for (size_t k = 0; k < self.K; k++) ordering.push_back(X(k));
// Eliminate partially i.e. only continuous part.
const auto [hybridBayesNet, remainingFactorGraph] =
linearizedFactorGraph.eliminatePartialSequential(ordering);
self.linearizedFactorGraph().eliminatePartialSequential(ordering);
CHECK(hybridBayesNet);
EXPECT_LONGS_EQUAL(3, hybridBayesNet->size());
@ -444,11 +442,11 @@ TEST(HybridNonlinearFactorGraph, PrintErrors) {
// Get nonlinear factor graph and add linear factors to be holistic.
// TODO(Frank): ???
HybridNonlinearFactorGraph fg = self.nonlinearFactorGraph();
fg.add(self.linearizedFactorGraph);
fg.add(self.linearizedFactorGraph());
// Optimize to get HybridValues
HybridBayesNet::shared_ptr bn =
self.linearizedFactorGraph.eliminateSequential();
self.linearizedFactorGraph().eliminateSequential();
HybridValues hv = bn->optimize();
// Print and verify
@ -465,8 +463,6 @@ TEST(HybridNonlinearFactorGraph, PrintErrors) {
TEST(HybridNonlinearFactorGraph, Full_Elimination) {
Switching self(3);
auto linearizedFactorGraph = self.linearizedFactorGraph;
// We first do a partial elimination
DiscreteBayesNet discreteBayesNet;
@ -477,15 +473,10 @@ TEST(HybridNonlinearFactorGraph, Full_Elimination) {
// Eliminate partially.
const auto [hybridBayesNet_partial, remainingFactorGraph_partial] =
linearizedFactorGraph.eliminatePartialSequential(ordering);
self.linearizedFactorGraph().eliminatePartialSequential(ordering);
DiscreteFactorGraph discrete_fg;
// TODO(Varun) Make this a function of HybridGaussianFactorGraph?
for (auto &factor : (*remainingFactorGraph_partial)) {
auto df = dynamic_pointer_cast<DiscreteFactor>(factor);
assert(df);
discrete_fg.push_back(df);
}
DiscreteFactorGraph discrete_fg =
remainingFactorGraph_partial->discreteFactors();
ordering.clear();
for (size_t k = 0; k < self.K - 1; k++) ordering.push_back(M(k));
@ -500,7 +491,7 @@ TEST(HybridNonlinearFactorGraph, Full_Elimination) {
// Eliminate partially.
HybridBayesNet::shared_ptr hybridBayesNet =
linearizedFactorGraph.eliminateSequential(ordering);
self.linearizedFactorGraph().eliminateSequential(ordering);
CHECK(hybridBayesNet);
EXPECT_LONGS_EQUAL(5, hybridBayesNet->size());
@ -533,7 +524,7 @@ TEST(HybridNonlinearFactorGraph, Full_Elimination) {
TEST(HybridNonlinearFactorGraph, Printing) {
Switching self(3);
auto linearizedFactorGraph = self.linearizedFactorGraph;
auto linearizedFactorGraph = self.linearizedFactorGraph();
// Create ordering.
Ordering ordering;
@ -556,6 +547,24 @@ GaussianFactor:
No noise model
Factor 1
GaussianFactor:
A[x1] = [
10
]
b = [ -10 ]
No noise model
Factor 2
GaussianFactor:
A[x2] = [
10
]
b = [ -10 ]
No noise model
Factor 3
HybridGaussianFactor:
Hybrid [x0 x1; m0]{
Choice(m0)
@ -583,7 +592,7 @@ scalar: 0.918939
}
Factor 2
Factor 4
HybridGaussianFactor:
Hybrid [x1 x2; m1]{
Choice(m1)
@ -611,24 +620,6 @@ scalar: 0.918939
}
Factor 3
GaussianFactor:
A[x1] = [
10
]
b = [ -10 ]
No noise model
Factor 4
GaussianFactor:
A[x2] = [
10
]
b = [ -10 ]
No noise model
Factor 5
DiscreteFactor:
P( m0 ):
@ -651,16 +642,38 @@ DiscreteFactor:
#else
string expected_hybridFactorGraph = R"(
size: 7
factor 0:
Factor 0
GaussianFactor:
A[x0] = [
10
]
b = [ -10 ]
No noise model
factor 1:
Factor 1
GaussianFactor:
A[x1] = [
10
]
b = [ -10 ]
No noise model
Factor 2
GaussianFactor:
A[x2] = [
10
]
b = [ -10 ]
No noise model
Factor 3
HybridGaussianFactor:
Hybrid [x0 x1; m0]{
Choice(m0)
0 Leaf:
0 Leaf :
A[x0] = [
-1
]
@ -669,8 +682,9 @@ Hybrid [x0 x1; m0]{
]
b = [ -1 ]
No noise model
scalar: 0.918939
1 Leaf:
1 Leaf :
A[x0] = [
-1
]
@ -679,12 +693,15 @@ Hybrid [x0 x1; m0]{
]
b = [ -0 ]
No noise model
scalar: 0.918939
}
factor 2:
Factor 4
HybridGaussianFactor:
Hybrid [x1 x2; m1]{
Choice(m1)
0 Leaf:
0 Leaf :
A[x1] = [
-1
]
@ -693,8 +710,9 @@ Hybrid [x1 x2; m1]{
]
b = [ -1 ]
No noise model
scalar: 0.918939
1 Leaf:
1 Leaf :
A[x1] = [
-1
]
@ -703,26 +721,21 @@ Hybrid [x1 x2; m1]{
]
b = [ -0 ]
No noise model
scalar: 0.918939
}
factor 3:
A[x1] = [
10
]
b = [ -10 ]
No noise model
factor 4:
A[x2] = [
10
]
b = [ -10 ]
No noise model
factor 5: P( m0 ):
Choice(m0)
0 Leaf 0.5
1 Leaf 0.5
factor 6: P( m1 | m0 ):
Factor 5
DiscreteFactor:
P( m0 ):
Choice(m0)
0 Leaf 0.5
1 Leaf 0.5
Factor 6
DiscreteFactor:
P( m1 | m0 ):
Choice(m1)
0 Choice(m0)
0 0 Leaf 0.33333333
@ -731,6 +744,7 @@ factor 6: P( m1 | m0 ):
1 0 Leaf 0.66666667
1 1 Leaf 0.4
)";
#endif

81
gtsam/hybrid/tests/testHybridNonlinearISAM.cpp
View File

@ -49,7 +49,7 @@ using symbol_shorthand::Z;
TEST(HybridNonlinearISAM, IncrementalElimination) {
Switching switching(3);
HybridNonlinearISAM isam;
HybridNonlinearFactorGraph graph1;
HybridNonlinearFactorGraph graph;
Values initial;
// Create initial factor graph
@ -57,17 +57,17 @@ TEST(HybridNonlinearISAM, IncrementalElimination) {
// | | |
// X0 -*- X1 -*- X2
// \*-M0-*/
graph1.push_back(switching.unaryFactors.at(0)); // P(X0)
graph1.push_back(switching.binaryFactors.at(0)); // P(X0, X1 | M0)
graph1.push_back(switching.binaryFactors.at(1)); // P(X1, X2 | M1)
graph1.push_back(switching.modeChain.at(0)); // P(M0)
graph.push_back(switching.unaryFactors.at(0)); // P(X0)
graph.push_back(switching.binaryFactors.at(0)); // P(X0, X1 | M0)
graph.push_back(switching.binaryFactors.at(1)); // P(X1, X2 | M1)
graph.push_back(switching.modeChain.at(0)); // P(M0)
initial.insert<double>(X(0), 1);
initial.insert<double>(X(1), 2);
initial.insert<double>(X(2), 3);
// Run update step
isam.update(graph1, initial);
isam.update(graph, initial);
// Check that after update we have 3 hybrid Bayes net nodes:
// P(X0 | X1, M0) and P(X1, X2 | M0, M1), P(M0, M1)
@ -80,14 +80,14 @@ TEST(HybridNonlinearISAM, IncrementalElimination) {
/********************************************************/
// New factor graph for incremental update.
HybridNonlinearFactorGraph graph2;
graph = HybridNonlinearFactorGraph();
initial = Values();
graph1.push_back(switching.unaryFactors.at(1)); // P(X1)
graph2.push_back(switching.unaryFactors.at(2)); // P(X2)
graph2.push_back(switching.modeChain.at(1)); // P(M0, M1)
graph.push_back(switching.unaryFactors.at(1)); // P(X1)
graph.push_back(switching.unaryFactors.at(2)); // P(X2)
graph.push_back(switching.modeChain.at(1)); // P(M0, M1)
isam.update(graph2, initial);
isam.update(graph, initial);
bayesTree = isam.bayesTree();
// Check that after the second update we have
@ -103,7 +103,7 @@ TEST(HybridNonlinearISAM, IncrementalElimination) {
TEST(HybridNonlinearISAM, IncrementalInference) {
Switching switching(3);
HybridNonlinearISAM isam;
HybridNonlinearFactorGraph graph1;
HybridNonlinearFactorGraph graph;
Values initial;
// Create initial factor graph
@ -112,16 +112,16 @@ TEST(HybridNonlinearISAM, IncrementalInference) {
// X0 -*- X1 -*- X2
// | |
// *-M0 - * - M1
graph1.push_back(switching.unaryFactors.at(0)); // P(X0)
graph1.push_back(switching.binaryFactors.at(0)); // P(X0, X1 | M0)
graph1.push_back(switching.unaryFactors.at(1)); // P(X1)
graph1.push_back(switching.modeChain.at(0)); // P(M0)
graph.push_back(switching.unaryFactors.at(0)); // P(X0)
graph.push_back(switching.binaryFactors.at(0)); // P(X0, X1 | M0)
graph.push_back(switching.unaryFactors.at(1)); // P(X1)
graph.push_back(switching.modeChain.at(0)); // P(M0)
initial.insert<double>(X(0), 1);
initial.insert<double>(X(1), 2);
// Run update step
isam.update(graph1, initial);
isam.update(graph, initial);
HybridGaussianISAM bayesTree = isam.bayesTree();
auto discreteConditional_m0 = bayesTree[M(0)]->conditional()->asDiscrete();
@ -129,16 +129,16 @@ TEST(HybridNonlinearISAM, IncrementalInference) {
/********************************************************/
// New factor graph for incremental update.
HybridNonlinearFactorGraph graph2;
graph = HybridNonlinearFactorGraph();
initial = Values();
initial.insert<double>(X(2), 3);
graph2.push_back(switching.binaryFactors.at(1)); // P(X1, X2 | M1)
graph2.push_back(switching.unaryFactors.at(2)); // P(X2)
graph2.push_back(switching.modeChain.at(1)); // P(M0, M1)
graph.push_back(switching.binaryFactors.at(1)); // P(X1, X2 | M1)
graph.push_back(switching.unaryFactors.at(2)); // P(X2)
graph.push_back(switching.modeChain.at(1)); // P(M0, M1)
isam.update(graph2, initial);
isam.update(graph, initial);
bayesTree = isam.bayesTree();
/********************************************************/
@ -147,7 +147,7 @@ TEST(HybridNonlinearISAM, IncrementalInference) {
// Now we calculate the actual factors using full elimination
const auto [expectedHybridBayesTree, expectedRemainingGraph] =
switching.linearizedFactorGraph
switching.linearizedFactorGraph()
.BaseEliminateable::eliminatePartialMultifrontal(ordering);
// The densities on X(1) should be the same
@ -195,27 +195,25 @@ TEST(HybridNonlinearISAM, IncrementalInference) {
}
/* ****************************************************************************/
// Test if we can approximately do the inference
TEST(HybridNonlinearISAM, Approx_inference) {
// Test if we can approximately do the inference (using pruning)
TEST(HybridNonlinearISAM, ApproxInference) {
Switching switching(4);
HybridNonlinearISAM incrementalHybrid;
HybridNonlinearFactorGraph graph1;
HybridNonlinearFactorGraph graph;
Values initial;
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
for (size_t i = 0; i < 3; i++) {
graph1.push_back(switching.binaryFactors.at(i));
graph.push_back(switching.binaryFactors.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
for (size_t i = 0; i < 4; i++) {
graph1.push_back(switching.unaryFactors.at(i));
graph.push_back(switching.unaryFactors.at(i));
initial.insert<double>(X(i), i + 1);
}
// TODO(Frank): no mode chain?
// Create ordering.
Ordering ordering;
for (size_t j = 0; j < 4; j++) {
@ -224,11 +222,11 @@ TEST(HybridNonlinearISAM, Approx_inference) {
// Now we calculate the actual factors using full elimination
const auto [unPrunedHybridBayesTree, unPrunedRemainingGraph] =
switching.linearizedFactorGraph
switching.linearizedFactorGraph()
.BaseEliminateable::eliminatePartialMultifrontal(ordering);
size_t maxNrLeaves = 5;
incrementalHybrid.update(graph1, initial);
incrementalHybrid.update(graph, initial);
HybridGaussianISAM bayesTree = incrementalHybrid.bayesTree();
bayesTree.prune(maxNrLeaves);
@ -304,31 +302,30 @@ TEST(HybridNonlinearISAM, Approx_inference) {
/* ****************************************************************************/
// Test approximate inference with an additional pruning step.
TEST(HybridNonlinearISAM, Incremental_approximate) {
TEST(HybridNonlinearISAM, IncrementalApproximate) {
Switching switching(5);
HybridNonlinearISAM incrementalHybrid;
HybridNonlinearFactorGraph graph1;
HybridNonlinearFactorGraph graph;
Values initial;
/***** Run Round 1 *****/
// Add the 3 hybrid factors, x0-x1, x1-x2, x2-x3
for (size_t i = 0; i < 3; i++) {
graph1.push_back(switching.binaryFactors.at(i));
graph.push_back(switching.binaryFactors.at(i));
}
// Add the Gaussian factors, 1 prior on X(0),
// 3 measurements on X(1), X(2), X(3)
for (size_t i = 0; i < 4; i++) {
graph1.push_back(switching.unaryFactors.at(i));
graph.push_back(switching.unaryFactors.at(i));
initial.insert<double>(X(i), i + 1);
}
// TODO(Frank): no mode chain?
// Run update with pruning
size_t maxComponents = 5;
incrementalHybrid.update(graph1, initial);
incrementalHybrid.update(graph, initial);
incrementalHybrid.prune(maxComponents);
HybridGaussianISAM bayesTree = incrementalHybrid.bayesTree();
@ -345,14 +342,14 @@ TEST(HybridNonlinearISAM, Incremental_approximate) {
5, bayesTree[X(3)]->conditional()->asHybrid()->nrComponents());
/***** Run Round 2 *****/
HybridGaussianFactorGraph graph2;
graph2.push_back(switching.binaryFactors.at(3)); // x3-x4
graph2.push_back(switching.unaryFactors.at(4)); // x4 measurement
graph = HybridGaussianFactorGraph();
graph.push_back(switching.binaryFactors.at(3)); // x3-x4
graph.push_back(switching.unaryFactors.at(4)); // x4 measurement
initial = Values();
initial.insert<double>(X(4), 5);
// Run update with pruning a second time.
incrementalHybrid.update(graph2, initial);
incrementalHybrid.update(graph, initial);
incrementalHybrid.prune(maxComponents);
bayesTree = incrementalHybrid.bayesTree();

4
gtsam/hybrid/tests/testSerializationHybrid.cpp
View File

@ -130,7 +130,7 @@ TEST(HybridSerialization, HybridGaussianConditional) {
// Test HybridBayesNet serialization.
TEST(HybridSerialization, HybridBayesNet) {
Switching s(2);
HybridBayesNet hbn = *(s.linearizedFactorGraph.eliminateSequential());
HybridBayesNet hbn = *(s.linearizedFactorGraph().eliminateSequential());
EXPECT(equalsObj<HybridBayesNet>(hbn));
EXPECT(equalsXML<HybridBayesNet>(hbn));
@ -141,7 +141,7 @@ TEST(HybridSerialization, HybridBayesNet) {
// Test HybridBayesTree serialization.
TEST(HybridSerialization, HybridBayesTree) {
Switching s(2);
HybridBayesTree hbt = *(s.linearizedFactorGraph.eliminateMultifrontal());
HybridBayesTree hbt = *(s.linearizedFactorGraph().eliminateMultifrontal());
EXPECT(equalsObj<HybridBayesTree>(hbt));
EXPECT(equalsXML<HybridBayesTree>(hbt));

5
gtsam/inference/EdgeKey.h
View File

@ -46,7 +46,10 @@ class GTSAM_EXPORT EdgeKey {
/// @{
/// Cast to Key
operator Key() const { return ((std::uint64_t)i_ << 32) | j_; }
Key key() const { return ((std::uint64_t)i_ << 32) | j_; }
/// Cast to Key
operator Key() const { return key(); }
/// Retrieve high 32 bits
inline std::uint32_t i() const { return i_; }

13
gtsam/inference/inference.i
View File

@ -96,6 +96,19 @@ unsigned char mrsymbolChr(size_t key);
unsigned char mrsymbolLabel(size_t key);
size_t mrsymbolIndex(size_t key);
#include <gtsam/inference/EdgeKey.h>
class EdgeKey {
EdgeKey(std::uint32_t i, std::uint32_t j);
EdgeKey(size_t key);
EdgeKey(const gtsam::EdgeKey& key);
std::uint32_t i() const;
std::uint32_t j() const;
size_t key() const;
void print(string s = "") const;
};
#include <gtsam/inference/Ordering.h>
class Ordering {
/// Type of ordering to use

5
gtsam/linear/VectorValues.cpp
View File

@ -22,8 +22,10 @@
#include <utility>
// assert_throw needs a semicolon in Release mode.
#if defined(__clang__)
#pragma clang diagnostic push
#pragma clang diagnostic ignored "-Wextra-semi-stmt"
#endif
namespace gtsam {
@ -417,5 +419,6 @@ namespace gtsam {
} // \namespace gtsam
#if defined(__clang__)
#pragma clang diagnostic pop
#endif

30
gtsam/navigation/AttitudeFactor.cpp
View File

@ -26,16 +26,16 @@ namespace gtsam {
Vector AttitudeFactor::attitudeError(const Rot3& nRb,
OptionalJacobian<2, 3> H) const {
if (H) {
Matrix23 D_nRef_R;
Matrix22 D_e_nRef;
Unit3 nRef = nRb.rotate(bRef_, D_nRef_R);
Vector e = nZ_.error(nRef, D_e_nRef);
Matrix23 D_nRotated_R;
Matrix22 D_e_nRotated;
Unit3 nRotated = nRb.rotate(bMeasured_, D_nRotated_R);
Vector e = nRef_.error(nRotated, D_e_nRotated);
(*H) = D_e_nRef * D_nRef_R;
(*H) = D_e_nRotated * D_nRotated_R;
return e;
} else {
Unit3 nRef = nRb * bRef_;
return nZ_.error(nRef);
Unit3 nRotated = nRb * bMeasured_;
return nRef_.error(nRotated);
}
}
@ -44,8 +44,8 @@ void Rot3AttitudeFactor::print(const string& s,
const KeyFormatter& keyFormatter) const {
cout << (s.empty() ? "" : s + " ") << "Rot3AttitudeFactor on "
<< keyFormatter(this->key()) << "\n";
nZ_.print(" measured direction in nav frame: ");
bRef_.print(" reference direction in body frame: ");
nRef_.print(" reference direction in nav frame: ");
bMeasured_.print(" measured direction in body frame: ");
this->noiseModel_->print(" noise model: ");
}
@ -53,16 +53,16 @@ void Rot3AttitudeFactor::print(const string& s,
bool Rot3AttitudeFactor::equals(const NonlinearFactor& expected,
double tol) const {
const This* e = dynamic_cast<const This*>(&expected);
return e != nullptr && Base::equals(*e, tol) && this->nZ_.equals(e->nZ_, tol)
&& this->bRef_.equals(e->bRef_, tol);
return e != nullptr && Base::equals(*e, tol) && this->nRef_.equals(e->nRef_, tol)
&& this->bMeasured_.equals(e->bMeasured_, tol);
}
//***************************************************************************
void Pose3AttitudeFactor::print(const string& s,
const KeyFormatter& keyFormatter) const {
cout << s << "Pose3AttitudeFactor on " << keyFormatter(this->key()) << "\n";
nZ_.print(" measured direction in nav frame: ");
bRef_.print(" reference direction in body frame: ");
nRef_.print(" reference direction in nav frame: ");
bMeasured_.print(" measured direction in body frame: ");
this->noiseModel_->print(" noise model: ");
}
@ -70,8 +70,8 @@ void Pose3AttitudeFactor::print(const string& s,
bool Pose3AttitudeFactor::equals(const NonlinearFactor& expected,
double tol) const {
const This* e = dynamic_cast<const This*>(&expected);
return e != nullptr && Base::equals(*e, tol) && this->nZ_.equals(e->nZ_, tol)
&& this->bRef_.equals(e->bRef_, tol);
return e != nullptr && Base::equals(*e, tol) && this->nRef_.equals(e->nRef_, tol)
&& this->bMeasured_.equals(e->bMeasured_, tol);
}
//***************************************************************************

172
gtsam/navigation/AttitudeFactor.h
View File

@ -17,59 +17,69 @@
**/
#pragma once
#include <gtsam/nonlinear/NonlinearFactor.h>
#include <gtsam/geometry/Pose3.h>
#include <gtsam/geometry/Unit3.h>
#include <gtsam/nonlinear/NonlinearFactor.h>
namespace gtsam {
/**
* Base class for prior on attitude
* Example:
* - measurement is direction of gravity in body frame bF
* - reference is direction of gravity in navigation frame nG
* This factor will give zero error if nRb * bF == nG
* @class AttitudeFactor
*
* @brief Base class for an attitude factor that constrains the rotation between
* body and navigation frames.
*
* This factor enforces that when the measured direction in the body frame
* (e.g., from an IMU accelerometer) is rotated into the navigation frame using the
* rotation variable, it should align with a known reference direction in the
* navigation frame (e.g., gravity vector).
*
* Mathematically, the error is zero when:
* nRb * bMeasured == nRef
*
* This is useful for incorporating absolute orientation measurements into the
* factor graph.
*
* @ingroup navigation
*/
class AttitudeFactor {
protected:
Unit3 nRef_, bMeasured_; ///< Position measurement in
protected:
Unit3 nZ_, bRef_; ///< Position measurement in
public:
public:
/** default constructor - only use for serialization */
AttitudeFactor() {
}
AttitudeFactor() {}
/**
* @brief Constructor
* @param nZ measured direction in navigation frame
* @param bRef reference direction in body frame (default Z-axis in NED frame, i.e., [0; 0; 1])
* @param nRef Reference direction in the navigation frame (e.g., gravity).
* @param bMeasured Measured direction in the body frame (e.g., from IMU
* accelerometer). Default is Unit3(0, 0, 1).
*/
AttitudeFactor(const Unit3& nZ, const Unit3& bRef = Unit3(0, 0, 1)) :
nZ_(nZ), bRef_(bRef) {
}
AttitudeFactor(const Unit3& nRef, const Unit3& bMeasured = Unit3(0, 0, 1))
: nRef_(nRef), bMeasured_(bMeasured) {}
/** vector of errors */
Vector attitudeError(const Rot3& p,
OptionalJacobian<2,3> H = {}) const;
Vector attitudeError(const Rot3& p, OptionalJacobian<2, 3> H = {}) const;
const Unit3& nZ() const {
return nZ_;
}
const Unit3& bRef() const {
return bRef_;
}
const Unit3& nRef() const { return nRef_; }
const Unit3& bMeasured() const { return bMeasured_; }
#ifdef GTSAM_ALLOW_DEPRECATED_SINCE_V43
[[deprecated("Use nRef() instead")]]
const Unit3& nZ() const { return nRef_; }
[[deprecated("Use bMeasured() instead")]]
const Unit3& bRef() const { return bMeasured_; }
#endif
#ifdef GTSAM_ENABLE_BOOST_SERIALIZATION
/** Serialization function */
friend class boost::serialization::access;
template<class ARCHIVE>
void serialize(ARCHIVE & ar, const unsigned int /*version*/) {
ar & boost::serialization::make_nvp("nZ_", nZ_);
ar & boost::serialization::make_nvp("bRef_", bRef_);
template <class ARCHIVE>
void serialize(ARCHIVE& ar, const unsigned int /*version*/) {
ar& boost::serialization::make_nvp("nRef_", nRef_);
ar& boost::serialization::make_nvp("bMeasured_", bMeasured_);
}
#endif
};
@ -78,12 +88,11 @@ public:
* Version of AttitudeFactor for Rot3
* @ingroup navigation
*/
class GTSAM_EXPORT Rot3AttitudeFactor: public NoiseModelFactorN<Rot3>, public AttitudeFactor {
class GTSAM_EXPORT Rot3AttitudeFactor : public NoiseModelFactorN<Rot3>,
public AttitudeFactor {
typedef NoiseModelFactorN<Rot3> Base;
public:
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
@ -94,23 +103,20 @@ public:
typedef Rot3AttitudeFactor This;
/** default constructor - only use for serialization */
Rot3AttitudeFactor() {
}
Rot3AttitudeFactor() {}
~Rot3AttitudeFactor() override {
}
~Rot3AttitudeFactor() override {}
/**
* @brief Constructor
* @param key of the Rot3 variable that will be constrained
* @param nZ measured direction in navigation frame
* @param nRef reference direction in navigation frame
* @param model Gaussian noise model
* @param bRef reference direction in body frame (default Z-axis)
* @param bMeasured measured direction in body frame (default Z-axis)
*/
Rot3AttitudeFactor(Key key, const Unit3& nZ, const SharedNoiseModel& model,
const Unit3& bRef = Unit3(0, 0, 1)) :
Base(model, key), AttitudeFactor(nZ, bRef) {
}
Rot3AttitudeFactor(Key key, const Unit3& nRef, const SharedNoiseModel& model,
const Unit3& bMeasured = Unit3(0, 0, 1))
: Base(model, key), AttitudeFactor(nRef, bMeasured) {}
/// @return a deep copy of this factor
gtsam::NonlinearFactor::shared_ptr clone() const override {
@ -123,46 +129,46 @@ public:
DefaultKeyFormatter) const override;
/** equals */
bool equals(const NonlinearFactor& expected, double tol = 1e-9) const override;
bool equals(const NonlinearFactor& expected,
double tol = 1e-9) const override;
/** vector of errors */
Vector evaluateError(const Rot3& nRb, OptionalMatrixType H) const override {
return attitudeError(nRb, H);
}
private:
private:
#ifdef GTSAM_ENABLE_BOOST_SERIALIZATION
/** Serialization function */
friend class boost::serialization::access;
template<class ARCHIVE>
void serialize(ARCHIVE & ar, const unsigned int /*version*/) {
template <class ARCHIVE>
void serialize(ARCHIVE& ar, const unsigned int /*version*/) {
// NoiseModelFactor1 instead of NoiseModelFactorN for backward compatibility
ar & boost::serialization::make_nvp("NoiseModelFactor1",
boost::serialization::base_object<Base>(*this));
ar & boost::serialization::make_nvp("AttitudeFactor",
ar& boost::serialization::make_nvp(
"NoiseModelFactor1", boost::serialization::base_object<Base>(*this));
ar& boost::serialization::make_nvp(
"AttitudeFactor",
boost::serialization::base_object<AttitudeFactor>(*this));
}
#endif
public:
public:
GTSAM_MAKE_ALIGNED_OPERATOR_NEW
};
/// traits
template<> struct traits<Rot3AttitudeFactor> : public Testable<Rot3AttitudeFactor> {};
template <>
struct traits<Rot3AttitudeFactor> : public Testable<Rot3AttitudeFactor> {};
/**
* Version of AttitudeFactor for Pose3
* @ingroup navigation
*/
class GTSAM_EXPORT Pose3AttitudeFactor: public NoiseModelFactorN<Pose3>,
public AttitudeFactor {
class GTSAM_EXPORT Pose3AttitudeFactor : public NoiseModelFactorN<Pose3>,
public AttitudeFactor {
typedef NoiseModelFactorN<Pose3> Base;
public:
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
@ -173,23 +179,20 @@ public:
typedef Pose3AttitudeFactor This;
/** default constructor - only use for serialization */
Pose3AttitudeFactor() {
}
Pose3AttitudeFactor() {}
~Pose3AttitudeFactor() override {
}
~Pose3AttitudeFactor() override {}
/**
* @brief Constructor
* @param key of the Pose3 variable that will be constrained
* @param nZ measured direction in navigation frame
* @param nRef reference direction in navigation frame
* @param model Gaussian noise model
* @param bRef reference direction in body frame (default Z-axis)
* @param bMeasured measured direction in body frame (default Z-axis)
*/
Pose3AttitudeFactor(Key key, const Unit3& nZ, const SharedNoiseModel& model,
const Unit3& bRef = Unit3(0, 0, 1)) :
Base(model, key), AttitudeFactor(nZ, bRef) {
}
Pose3AttitudeFactor(Key key, const Unit3& nRef, const SharedNoiseModel& model,
const Unit3& bMeasured = Unit3(0, 0, 1))
: Base(model, key), AttitudeFactor(nRef, bMeasured) {}
/// @return a deep copy of this factor
gtsam::NonlinearFactor::shared_ptr clone() const override {
@ -202,40 +205,41 @@ public:
DefaultKeyFormatter) const override;
/** equals */
bool equals(const NonlinearFactor& expected, double tol = 1e-9) const override;
bool equals(const NonlinearFactor& expected,
double tol = 1e-9) const override;
/** vector of errors */
Vector evaluateError(const Pose3& nTb, OptionalMatrixType H) const override {
Vector e = attitudeError(nTb.rotation(), H);
if (H) {
Matrix H23 = *H;
*H = Matrix::Zero(2,6);
H->block<2,3>(0,0) = H23;
*H = Matrix::Zero(2, 6);
H->block<2, 3>(0, 0) = H23;
}
return e;
}
private:
private:
#ifdef GTSAM_ENABLE_BOOST_SERIALIZATION
/** Serialization function */
friend class boost::serialization::access;
template<class ARCHIVE>
void serialize(ARCHIVE & ar, const unsigned int /*version*/) {
template <class ARCHIVE>
void serialize(ARCHIVE& ar, const unsigned int /*version*/) {
// NoiseModelFactor1 instead of NoiseModelFactorN for backward compatibility
ar & boost::serialization::make_nvp("NoiseModelFactor1",
boost::serialization::base_object<Base>(*this));
ar & boost::serialization::make_nvp("AttitudeFactor",
ar& boost::serialization::make_nvp(
"NoiseModelFactor1", boost::serialization::base_object<Base>(*this));
ar& boost::serialization::make_nvp(
"AttitudeFactor",
boost::serialization::base_object<AttitudeFactor>(*this));
}
#endif
public:
public:
GTSAM_MAKE_ALIGNED_OPERATOR_NEW
};
/// traits
template<> struct traits<Pose3AttitudeFactor> : public Testable<Pose3AttitudeFactor> {};
} /// namespace gtsam
template <>
struct traits<Pose3AttitudeFactor> : public Testable<Pose3AttitudeFactor> {};
} // namespace gtsam

136
gtsam/navigation/AttitudeFactor.md Normal file
View File

@ -0,0 +1,136 @@
# AttitudeFactor in GTSAM
[Cautionary note: this was generated from the source using ChatGPT but edited by Frank]
## Introduction
The `AttitudeFactor` in GTSAM is a factor that constrains the orientation (attitude) of a robot or sensor platform based on directional measurements. This is particularly useful in GPS-denied navigation contexts where orientation must be estimated from inertial sensors like accelerometers or magnetometers.
This document explains the mathematical foundation of the `AttitudeFactor` and guides users on how to use this factor effectively in GTSAM.
## Mathematical Foundation
### Concept
The `AttitudeFactor` constrains the rotation $\mathbf{R}_{nb}$ (from body frame $b$ to navigation frame $n$) such that a known reference direction in the navigation frame aligns with a measured direction in the body frame, when rotated. The factor enforces that:
$$
\text{nRef} \approx \mathbf{R}_{nb} \cdot \text{bMeasured}
$$
where:
- $\mathbf{R}_{nb}$ is the rotation matrix representing the orientation from body to navigation frame.
- $\text{bMeasured}$ is the measured direction in the body frame (e.g., the accelerometer reading).
- $\text{nRef}$ is the known reference direction in the navigation frame (e.g., the gravity vector in nav).
### Error Function
The error function computes the angular difference between the rotated reference direction and the measured direction:
$$
\mathbf{e} = \text{error}(\text{nRef}, \mathbf{R}_{nb} \cdot \text{bMeasured})
$$
This error is minimal (zero) when the rotated body reference direction aligns perfectly with the measured navigation direction.
The error is computed internally using the `attitudeError` function:
```cpp
Vector AttitudeFactor::attitudeError(const Rot3& nRb) const {
Unit3 nRotated = nRb * bMeasured_;
return nRef_.error(nRotated);
}
```
#### Explanation:
- The function computes the rotated measurement `nRotated` and then the error between `nRef` and `nRotated`.
- `nRef_.error(nRotated)` is a 2D vector-valued error between two directions, defined in [Unit3.h](../geometry/Unit3.h).
### Jacobians
For optimization, the $2 \times 3$ Jacobian of the error function with respect to the rotation parameters is required. The Jacobian is computed using chain rule differentiation, involving the derivative of the rotated vector with respect to the rotation parameters and the derivative of the error with respect to the rotated vector.
Note the Jacobian for this specific error function vanishes 180 degrees away from the true direction, and the factor is only expected to behave well when the `nRb` value is initialized in the correct hemisphere.
## Usage in GTSAM
### Including the Header
Include the `AttitudeFactor.h` header in your code:
```cpp
#include <gtsam/navigation/AttitudeFactor.h>
```
### Creating an Attitude Factor
You can create an attitude factor for either a `Rot3` (rotation only) or a `Pose3` (position and rotation) variable.
#### For `Rot3` Variables
```cpp
// Define keys
gtsam::Key rotKey = ...;
// Known reference direction in navigation frame (e.g., gravity)
gtsam::Unit3 nRef(0, 0, -1); // Assuming gravity points down in navigation frame
// Measured direction in body frame (e.g., accelerometer direction)
gtsam::Unit3 bMeasured(0, 0, 9.8); // will be normalized automatically
// Noise model
auto noiseModel = gtsam::noiseModel::Isotropic::Sigma(2, 0.1); // 2D error, sigma = 0.1
// Add to factor graph
gtsam::NonlinearFactorGraph graph;
graph.emplace_shared<Rot3AttitudeFactor>(rotKey, nRef, noiseModel, bMeasured);
```
#### For `Pose3` Variables
There is also a `Pose3AttitudeFactor` that automatically extracts the rotation from the pose, taking into account the chain rule for this operation so the Jacobians with respect to pose are correct.
The same caveat about vanishing Jacobian holds.
```cpp
// Define keys
gtsam::Key poseKey = ...;
// Known reference direction in navigation frame (e.g., gravity)
gtsam::Unit3 nRef(0, 0, -1); // Assuming gravity points down in navigation frame
// Measured direction in body frame (e.g., accelerometer direction)
gtsam::Unit3 bMeasured(0, 0, 9.8); // will be normalized automatically
// Noise model
auto noiseModel = gtsam::noiseModel::Isotropic::Sigma(2, 0.1);
// Add to factor graph
gtsam::NonlinearFactorGraph graph;
graph.emplace_shared<Pose3AttitudeFactor>(poseKey, nRef, noiseModel, bMeasured);
```
### Explanation of Parameters
- **Key**: The variable key in the factor graph corresponding to the `Rot3` or `Pose3` variable you are constraining.
- **nRef**: The known direction in the navigation frame. This is typically obtained from sensors like accelerometers or magnetometers.
- **bMeasured**: The measured direction in the body frame. By default, this is set to the Z-axis `[0; 0; 1]`, but it should match the direction your sensor measures. When constructing a `Unit3`, will be automatically normalized.
- **noiseModel**: The noise model representing the uncertainty in the measurement. Adjust the standard deviation based on the confidence in your measurements.
## Example in GPS-Denied Navigation
In GPS-denied environments, orientation estimation relies heavily on inertial measurements. By incorporating the `AttitudeFactor`, you can:
- Constrain the roll and pitch angles using gravity measurements from an accelerometer.
- Constrain the yaw angle using magnetic field measurements from a magnetometer (with caution due to magnetic disturbances).
This factor helps maintain an accurate orientation estimate over time, which is crucial for applications like drone flight, underwater vehicles, or indoor robotics.
## Conclusion
The `AttitudeFactor` is a useful tool in GTSAM for incorporating orientation measurements into your factor graph. By aligning a measured direction in the body frame with a known reference direction in the navigation frame, it provides a constraint that improves the estimation of the rotation variable. Correct understanding and usage of this factor enhance the performance of navigation algorithms, especially in challenging environments where GPS is unavailable.
# References
- [GTSAM Documentation](https://gtsam.org/)
- [Unit3 Class Reference](https://gtsam.org/doxygen/)

14
gtsam/navigation/ImuFactor.h
View File

@ -37,13 +37,9 @@ typedef ManifoldPreintegration PreintegrationType;
/*
* If you are using the factor, please cite:
* L. Carlone, Z. Kira, C. Beall, V. Indelman, F. Dellaert, "Eliminating
* conditionally independent sets in factor graphs: a unifying perspective based
* on smart factors", Int. Conf. on Robotics and Automation (ICRA), 2014.
*
* C. Forster, L. Carlone, F. Dellaert, D. Scaramuzza, "IMU Preintegration on
* Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation",
* Robotics: Science and Systems (RSS), 2015.
* Christian Forster, Luca Carlone, Frank Dellaert, and Davide Scaramuzza,
* "On-Manifold Preintegration for Real-Time Visual-Inertial Odometry", IEEE
* Transactions on Robotics, 2017.
*
* REFERENCES:
* [1] G.S. Chirikjian, "Stochastic Models, Information Theory, and Lie Groups",
@ -54,8 +50,8 @@ typedef ManifoldPreintegration PreintegrationType;
* [3] L. Carlone, S. Williams, R. Roberts, "Preintegrated IMU factor:
* Computation of the Jacobian Matrices", Tech. Report, 2013.
* Available in this repo as "PreintegratedIMUJacobians.pdf".
* [4] C. Forster, L. Carlone, F. Dellaert, D. Scaramuzza, "IMU Preintegration on
* Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation",
* [4] C. Forster, L. Carlone, F. Dellaert, D. Scaramuzza, "IMU Preintegration
* on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation",
* Robotics: Science and Systems (RSS), 2015.
*/

42
gtsam/navigation/README.md Normal file
View File

@ -0,0 +1,42 @@
# Navigation Factors
This directory contains factors related to navigation, including various IMU factors.
## IMU Factor:
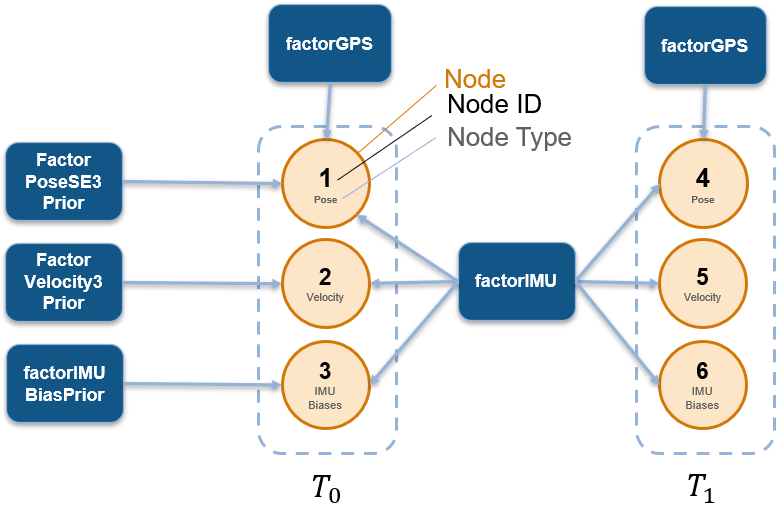
![IMU Factor Diagram](https://www.mathworks.com/help/examples/shared_positioning/win64/FactorGraphPedestrianIMUGPSLocalizationExample_02.png)
The `ImuFactor` is a 5-ways factor involving previous state (pose and velocity of
the vehicle at previous time step), current state (pose and velocity at
current time step), and the bias estimate.
Following the preintegration
scheme proposed in [2], the `ImuFactor` includes many IMU measurements, which
are "summarized" using the PreintegratedIMUMeasurements class.
The figure above, courtesy of [Mathworks' navigation toolbox](https://www.mathworks.com/help/nav/index.html), which are also using our work, shows the factor graph fragment for two time slices.
Note that this factor does not model "temporal consistency" of the biases
(which are usually slowly varying quantities), which is up to the caller.
See also `CombinedImuFactor` for a class that does this for you.
If you are using the factor, please cite:
> Christian Forster, Luca Carlone, Frank Dellaert, and Davide Scaramuzza, "On-Manifold Preintegration for Real-Time Visual-Inertial Odometry", IEEE Transactions on Robotics, 2017.
## REFERENCES:
1. G.S. Chirikjian, "Stochastic Models, Information Theory, and Lie Groups",
Volume 2, 2008.
2. T. Lupton and S.Sukkarieh, "Visual-Inertial-Aided Navigation for
High-Dynamic Motion in Built Environments Without Initial Conditions",
TRO, 28(1):61-76, 2012.
3. L. Carlone, S. Williams, R. Roberts, "Preintegrated IMU factor:
Computation of the Jacobian Matrices", Tech. Report, 2013.
Available in this repo as "PreintegratedIMUJacobians.pdf".
4. C. Forster, L. Carlone, F. Dellaert, D. Scaramuzza, "IMU Preintegration on
Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation",
Robotics: Science and Systems (RSS), 2015.
## The Attitude Factor
The `AttitudeFactor` in GTSAM is a factor that constrains the orientation (attitude) of a robot or sensor platform based on directional measurements. Both `Rot3` and `Pose3` versions are available.
Written up in detail with the help of ChatGPT [here](AttitudeFactor.md).

28
gtsam/navigation/navigation.i
View File

@ -256,34 +256,30 @@ virtual class AHRSFactor : gtsam::NonlinearFactor {
};
#include <gtsam/navigation/AttitudeFactor.h>
//virtual class AttitudeFactor : gtsam::NonlinearFactor {
// AttitudeFactor(const Unit3& nZ, const Unit3& bRef);
// AttitudeFactor();
//};
virtual class Rot3AttitudeFactor : gtsam::NonlinearFactor{
Rot3AttitudeFactor(size_t key, const gtsam::Unit3& nZ, const gtsam::noiseModel::Diagonal* model,
const gtsam::Unit3& bRef);
Rot3AttitudeFactor(size_t key, const gtsam::Unit3& nZ, const gtsam::noiseModel::Diagonal* model);
virtual class Rot3AttitudeFactor : gtsam::NoiseModelFactor {
Rot3AttitudeFactor(size_t key, const gtsam::Unit3& nRef, const gtsam::noiseModel::Diagonal* model,
const gtsam::Unit3& bMeasured);
Rot3AttitudeFactor(size_t key, const gtsam::Unit3& nRef, const gtsam::noiseModel::Diagonal* model);
Rot3AttitudeFactor();
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
bool equals(const gtsam::NonlinearFactor& expected, double tol) const;
gtsam::Unit3 nZ() const;
gtsam::Unit3 bRef() const;
gtsam::Unit3 nRef() const;
gtsam::Unit3 bMeasured() const;
};
virtual class Pose3AttitudeFactor : gtsam::NonlinearFactor {
Pose3AttitudeFactor(size_t key, const gtsam::Unit3& nZ,
virtual class Pose3AttitudeFactor : gtsam::NoiseModelFactor {
Pose3AttitudeFactor(size_t key, const gtsam::Unit3& nRef,
const gtsam::noiseModel::Diagonal* model,
const gtsam::Unit3& bRef);
Pose3AttitudeFactor(size_t key, const gtsam::Unit3& nZ,
const gtsam::Unit3& bMeasured);
Pose3AttitudeFactor(size_t key, const gtsam::Unit3& nRef,
const gtsam::noiseModel::Diagonal* model);
Pose3AttitudeFactor();
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
bool equals(const gtsam::NonlinearFactor& expected, double tol) const;
gtsam::Unit3 nZ() const;
gtsam::Unit3 bRef() const;
gtsam::Unit3 nRef() const;
gtsam::Unit3 bMeasured() const;
};
#include <gtsam/navigation/GPSFactor.h>

39
gtsam/navigation/tests/testAttitudeFactor.cpp
View File

@ -11,44 +11,44 @@
/**
* @file testAttitudeFactor.cpp
* @brief Unit test for Rot3AttitudeFactor
* @brief Unit test for AttitudeFactors (rot3 and Pose3 versions)
* @author Frank Dellaert
* @date January 22, 2014
*/
#include <gtsam/navigation/AttitudeFactor.h>
#include <CppUnitLite/TestHarness.h>
#include <gtsam/base/Testable.h>
#include <gtsam/base/numericalDerivative.h>
#include <gtsam/navigation/AttitudeFactor.h>
#include <functional>
#include "gtsam/base/Matrix.h"
#include <CppUnitLite/TestHarness.h>
using namespace std::placeholders;
using namespace std;
using namespace gtsam;
// *************************************************************************
TEST( Rot3AttitudeFactor, Constructor ) {
TEST(Rot3AttitudeFactor, Constructor) {
// Example: pitch and roll of aircraft in an ENU Cartesian frame.
// If pitch and roll are zero for an aerospace frame,
// that means Z is pointing down, i.e., direction of Z = (0,0,-1)
Unit3 bZ(0, 0, 1); // reference direction is body Z axis
Unit3 nDown(0, 0, -1); // down, in ENU navigation frame, is "measurement"
Unit3 bMeasured(0, 0, 1); // measured direction is body Z axis
Unit3 nDown(0, 0, -1); // down, in ENU navigation frame, is "reference"
// Factor
Key key(1);
SharedNoiseModel model = noiseModel::Isotropic::Sigma(2, 0.25);
Rot3AttitudeFactor factor0(key, nDown, model);
Rot3AttitudeFactor factor(key, nDown, model, bZ);
EXPECT(assert_equal(factor0,factor,1e-5));
Rot3AttitudeFactor factor(key, nDown, model, bMeasured);
EXPECT(assert_equal(factor0, factor, 1e-5));
// Create a linearization point at the zero-error point
Rot3 nRb;
EXPECT(assert_equal((Vector) Z_2x1,factor.evaluateError(nRb),1e-5));
EXPECT(assert_equal((Vector)Z_2x1, factor.evaluateError(nRb), 1e-5));
auto err_fn = [&factor](const Rot3& r){
auto err_fn = [&factor](const Rot3& r) {
return factor.evaluateError(r, OptionalNone);
};
// Calculate numerical derivatives
@ -80,32 +80,31 @@ TEST(Rot3AttitudeFactor, CopyAndMove) {
}
// *************************************************************************
TEST( Pose3AttitudeFactor, Constructor ) {
TEST(Pose3AttitudeFactor, Constructor) {
// Example: pitch and roll of aircraft in an ENU Cartesian frame.
// If pitch and roll are zero for an aerospace frame,
// that means Z is pointing down, i.e., direction of Z = (0,0,-1)
Unit3 bZ(0, 0, 1); // reference direction is body Z axis
Unit3 nDown(0, 0, -1); // down, in ENU navigation frame, is "measurement"
Unit3 bMeasured(0, 0, 1); // measured direction is body Z axis
Unit3 nDown(0, 0, -1); // down, in ENU navigation frame, is "reference"
// Factor
Key key(1);
SharedNoiseModel model = noiseModel::Isotropic::Sigma(2, 0.25);
Pose3AttitudeFactor factor0(key, nDown, model);
Pose3AttitudeFactor factor(key, nDown, model, bZ);
EXPECT(assert_equal(factor0,factor,1e-5));
Pose3AttitudeFactor factor(key, nDown, model, bMeasured);
EXPECT(assert_equal(factor0, factor, 1e-5));
// Create a linearization point at the zero-error point
Pose3 T(Rot3(), Point3(-5.0, 8.0, -11.0));
EXPECT(assert_equal((Vector) Z_2x1,factor.evaluateError(T),1e-5));
EXPECT(assert_equal((Vector)Z_2x1, factor.evaluateError(T), 1e-5));
Matrix actualH1;
auto err_fn = [&factor](const Pose3& p){
auto err_fn = [&factor](const Pose3& p) {
return factor.evaluateError(p, OptionalNone);
};
// Calculate numerical derivatives
Matrix expectedH = numericalDerivative11<Vector,Pose3>(err_fn, T);
Matrix expectedH = numericalDerivative11<Vector, Pose3>(err_fn, T);
// Use the factor to calculate the derivative
Matrix actualH;

5
gtsam/nonlinear/NonlinearConjugateGradientOptimizer.h
View File

@ -21,6 +21,8 @@
#include <gtsam/base/Manifold.h>
#include <gtsam/nonlinear/NonlinearOptimizer.h>
#include <stdexcept>
namespace gtsam {
/// Fletcher-Reeves formula for computing β, the direction of steepest descent.
@ -247,6 +249,9 @@ std::tuple<V, int> nonlinearConjugateGradient(
case DirectionMethod::DaiYuan:
beta = DaiYuan(currentGradient, prevGradient, direction);
break;
default:
throw std::runtime_error(
"NonlinearConjugateGradientOptimizer: Invalid directionMethod");
}
direction = currentGradient + (beta * direction);

2
gtsam/nonlinear/Values.h
View File

@ -189,7 +189,7 @@ namespace gtsam {
const_iterator_type it_;
deref_iterator(const_iterator_type it) : it_(it) {}
ConstKeyValuePair operator*() const { return {it_->first, *(it_->second)}; }
std::unique_ptr<ConstKeyValuePair> operator->() {
std::unique_ptr<ConstKeyValuePair> operator->() const {
return std::make_unique<ConstKeyValuePair>(it_->first, *(it_->second));
}
bool operator==(const deref_iterator& other) const {

14
gtsam/nonlinear/nonlinear.i
View File

@ -11,6 +11,7 @@ namespace gtsam {
#include <gtsam/geometry/Cal3_S2.h>
#include <gtsam/geometry/CalibratedCamera.h>
#include <gtsam/geometry/EssentialMatrix.h>
#include <gtsam/geometry/FundamentalMatrix.h>
#include <gtsam/geometry/PinholeCamera.h>
#include <gtsam/geometry/Point2.h>
#include <gtsam/geometry/Point3.h>
@ -74,13 +75,20 @@ class NonlinearFactorGraph {
gtsam::Pose2,
gtsam::Pose3,
gtsam::Cal3_S2,
gtsam::Cal3f,
gtsam::Cal3Bundler,
gtsam::Cal3Fisheye,
gtsam::Cal3Unified,
gtsam::CalibratedCamera,
gtsam::EssentialMatrix,
gtsam::FundamentalMatrix,
gtsam::SimpleFundamentalMatrix,
gtsam::PinholeCamera<gtsam::Cal3_S2>,
gtsam::PinholeCamera<gtsam::Cal3f>,
gtsam::PinholeCamera<gtsam::Cal3Bundler>,
gtsam::PinholeCamera<gtsam::Cal3Fisheye>,
gtsam::PinholeCamera<gtsam::Cal3Unified>,
gtsam::PinholeCamera<gtsam::CalibratedCamera>,
gtsam::imuBias::ConstantBias}>
void addPrior(size_t key, const T& prior,
const gtsam::noiseModel::Base* noiseModel);
@ -536,7 +544,8 @@ class ISAM2 {
gtsam::Values calculateEstimate() const;
template <VALUE = {gtsam::Point2, gtsam::Rot2, gtsam::Pose2, gtsam::Point3,
gtsam::Rot3, gtsam::Pose3, gtsam::Cal3_S2, gtsam::Cal3DS2,
gtsam::Cal3Bundler, gtsam::EssentialMatrix,
gtsam::Cal3f, gtsam::Cal3Bundler,
gtsam::EssentialMatrix, gtsam::FundamentalMatrix, gtsam::SimpleFundamentalMatrix,
gtsam::PinholeCamera<gtsam::Cal3_S2>,
gtsam::PinholeCamera<gtsam::Cal3Bundler>,
gtsam::PinholeCamera<gtsam::Cal3Fisheye>,
@ -706,6 +715,9 @@ virtual class BatchFixedLagSmoother : gtsam::FixedLagSmoother {
void print(string s = "BatchFixedLagSmoother:\n") const;
gtsam::LevenbergMarquardtParams params() const;
gtsam::NonlinearFactorGraph getFactors() const;
template <VALUE = {gtsam::Point2, gtsam::Rot2, gtsam::Pose2, gtsam::Point3,
gtsam::Rot3, gtsam::Pose3, gtsam::Cal3_S2, gtsam::Cal3DS2,
gtsam::Vector, gtsam::Matrix}>

91
gtsam/nonlinear/values.i
View File

@ -4,13 +4,14 @@
namespace gtsam {
#include <gtsam/geometry/Cal3_S2.h>
#include <gtsam/geometry/Cal3Bundler.h>
#include <gtsam/geometry/Cal3DS2.h>
#include <gtsam/geometry/Cal3f.h>
#include <gtsam/geometry/Cal3Fisheye.h>
#include <gtsam/geometry/Cal3Unified.h>
#include <gtsam/geometry/Cal3_S2.h>
#include <gtsam/geometry/CalibratedCamera.h>
#include <gtsam/geometry/EssentialMatrix.h>
#include <gtsam/geometry/FundamentalMatrix.h>
#include <gtsam/geometry/PinholeCamera.h>
#include <gtsam/geometry/Point2.h>
#include <gtsam/geometry/Point3.h>
@ -67,7 +68,7 @@ class Values {
// gtsam::Value at(size_t j) const;
// The order is important: gtsam::Vector has to precede Point2/Point3 so `atVector`
// can work for those fixed-size vectors.
// can work for those fixed-size vectors. Same apparently for Cal3Bundler and Cal3f.
void insert(size_t j, gtsam::Vector vector);
void insert(size_t j, gtsam::Matrix matrix);
void insert(size_t j, const gtsam::Point2& point2);
@ -80,18 +81,25 @@ class Values {
void insert(size_t j, const gtsam::Rot3& rot3);
void insert(size_t j, const gtsam::Pose3& pose3);
void insert(size_t j, const gtsam::Unit3& unit3);
void insert(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void insert(size_t j, const gtsam::Cal3f& cal3f);
void insert(size_t j, const gtsam::Cal3_S2& cal3_s2);
void insert(size_t j, const gtsam::Cal3DS2& cal3ds2);
void insert(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void insert(size_t j, const gtsam::Cal3Fisheye& cal3fisheye);
void insert(size_t j, const gtsam::Cal3Unified& cal3unified);
void insert(size_t j, const gtsam::EssentialMatrix& essential_matrix);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void insert(size_t j, const gtsam::EssentialMatrix& E);
void insert(size_t j, const gtsam::FundamentalMatrix& F);
void insert(size_t j, const gtsam::SimpleFundamentalMatrix& F);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Bundler>& camera);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3f>& camera);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3DS2>& camera);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Fisheye>& camera);
void insert(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Unified>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3Bundler>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3f>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3DS2>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3Fisheye>& camera);
void insert(size_t j, const gtsam::PinholePose<gtsam::Cal3Unified>& camera);
void insert(size_t j, const gtsam::imuBias::ConstantBias& constant_bias);
@ -115,18 +123,25 @@ class Values {
void update(size_t j, const gtsam::Rot3& rot3);
void update(size_t j, const gtsam::Pose3& pose3);
void update(size_t j, const gtsam::Unit3& unit3);
void update(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void update(size_t j, const gtsam::Cal3f& cal3f);
void update(size_t j, const gtsam::Cal3_S2& cal3_s2);
void update(size_t j, const gtsam::Cal3DS2& cal3ds2);
void update(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void update(size_t j, const gtsam::Cal3Fisheye& cal3fisheye);
void update(size_t j, const gtsam::Cal3Unified& cal3unified);
void update(size_t j, const gtsam::EssentialMatrix& essential_matrix);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void update(size_t j, const gtsam::EssentialMatrix& E);
void update(size_t j, const gtsam::FundamentalMatrix& F);
void update(size_t j, const gtsam::SimpleFundamentalMatrix& F);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Bundler>& camera);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3f>& camera);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3DS2>& camera);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Fisheye>& camera);
void update(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Unified>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3Bundler>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3f>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3DS2>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3Fisheye>& camera);
void update(size_t j, const gtsam::PinholePose<gtsam::Cal3Unified>& camera);
void update(size_t j, const gtsam::imuBias::ConstantBias& constant_bias);
@ -147,31 +162,28 @@ class Values {
void insert_or_assign(size_t j, const gtsam::Rot3& rot3);
void insert_or_assign(size_t j, const gtsam::Pose3& pose3);
void insert_or_assign(size_t j, const gtsam::Unit3& unit3);
void insert_or_assign(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void insert_or_assign(size_t j, const gtsam::Cal3f& cal3f);
void insert_or_assign(size_t j, const gtsam::Cal3_S2& cal3_s2);
void insert_or_assign(size_t j, const gtsam::Cal3DS2& cal3ds2);
void insert_or_assign(size_t j, const gtsam::Cal3Bundler& cal3bundler);
void insert_or_assign(size_t j, const gtsam::Cal3Fisheye& cal3fisheye);
void insert_or_assign(size_t j, const gtsam::Cal3Unified& cal3unified);
void insert_or_assign(size_t j,
const gtsam::EssentialMatrix& essential_matrix);
void insert_or_assign(size_t j,
const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholeCamera<gtsam::Cal3Bundler>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholeCamera<gtsam::Cal3Fisheye>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholeCamera<gtsam::Cal3Unified>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholePose<gtsam::Cal3Bundler>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholePose<gtsam::Cal3Fisheye>& camera);
void insert_or_assign(size_t j,
const gtsam::PinholePose<gtsam::Cal3Unified>& camera);
void insert_or_assign(size_t j,
const gtsam::imuBias::ConstantBias& constant_bias);
void insert_or_assign(size_t j, const gtsam::EssentialMatrix& E);
void insert_or_assign(size_t j, const gtsam::FundamentalMatrix& F);
void insert_or_assign(size_t j, const gtsam::SimpleFundamentalMatrix& F);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Bundler>& camera);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3f>& camera);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3_S2>& camera);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3DS2>& camera);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Fisheye>& camera);
void insert_or_assign(size_t j, const gtsam::PinholeCamera<gtsam::Cal3Unified>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3Bundler>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3f>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3_S2>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3DS2>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3Fisheye>& camera);
void insert_or_assign(size_t j, const gtsam::PinholePose<gtsam::Cal3Unified>& camera);
void insert_or_assign(size_t j, const gtsam::imuBias::ConstantBias& constant_bias);
void insert_or_assign(size_t j, const gtsam::NavState& nav_state);
void insert_or_assign(size_t j, double c);
@ -185,18 +197,25 @@ class Values {
gtsam::Rot3,
gtsam::Pose3,
gtsam::Unit3,
gtsam::Cal3Bundler,
gtsam::Cal3f,
gtsam::Cal3_S2,
gtsam::Cal3DS2,
gtsam::Cal3Bundler,
gtsam::Cal3Fisheye,
gtsam::Cal3Unified,
gtsam::EssentialMatrix,
gtsam::PinholeCamera<gtsam::Cal3_S2>,
gtsam::EssentialMatrix,
gtsam::FundamentalMatrix,
gtsam::SimpleFundamentalMatrix,
gtsam::PinholeCamera<gtsam::Cal3Bundler>,
gtsam::PinholeCamera<gtsam::Cal3f>,
gtsam::PinholeCamera<gtsam::Cal3_S2>,
gtsam::PinholeCamera<gtsam::Cal3DS2>,
gtsam::PinholeCamera<gtsam::Cal3Fisheye>,
gtsam::PinholeCamera<gtsam::Cal3Unified>,
gtsam::PinholePose<gtsam::Cal3_S2>,
gtsam::PinholePose<gtsam::Cal3Bundler>,
gtsam::PinholePose<gtsam::Cal3f>,
gtsam::PinholePose<gtsam::Cal3_S2>,
gtsam::PinholePose<gtsam::Cal3DS2>,
gtsam::PinholePose<gtsam::Cal3Fisheye>,
gtsam::PinholePose<gtsam::Cal3Unified>,
gtsam::imuBias::ConstantBias,

328
gtsam/sfm/TransferFactor.h
View File

@ -16,12 +16,66 @@
#pragma once
#include <gtsam/base/numericalDerivative.h>
#include <gtsam/geometry/EssentialMatrix.h>
#include <gtsam/geometry/FundamentalMatrix.h>
#include <gtsam/inference/EdgeKey.h>
#include <gtsam/inference/Symbol.h>
#include <gtsam/nonlinear/NonlinearFactor.h>
#include <cstdint>
namespace gtsam {
/**
* Base class that holds the EdgeKeys and provides the getMatrices method.
*/
template <typename F>
class TransferEdges {
protected:
EdgeKey edge1_, edge2_; ///< The two EdgeKeys.
uint32_t c_; ///< The transfer target
public:
TransferEdges(EdgeKey edge1, EdgeKey edge2)
: edge1_(edge1), edge2_(edge2), c_(ViewC(edge1, edge2)) {}
/// Returns the view A index based on the EdgeKeys
static size_t ViewA(const EdgeKey& edge1, const EdgeKey& edge2) {
size_t c = ViewC(edge1, edge2);
return (edge1.i() == c) ? edge1.j() : edge1.i();
}
/// Returns the view B index based on the EdgeKeys
static size_t ViewB(const EdgeKey& edge1, const EdgeKey& edge2) {
size_t c = ViewC(edge1, edge2);
return (edge2.i() == c) ? edge2.j() : edge2.i();
}
/// Returns the view C index based on the EdgeKeys
static size_t ViewC(const EdgeKey& edge1, const EdgeKey& edge2) {
if (edge1.i() == edge2.i() || edge1.i() == edge2.j())
return edge1.i();
else if (edge1.j() == edge2.i() || edge1.j() == edge2.j())
return edge1.j();
else
throw std::runtime_error(
"EssentialTransferFactorK: No common key in edge keys.");
}
/// Create Matrix3 objects based on EdgeKey configurations.
std::pair<Matrix3, Matrix3> getMatrices(const F& F1, const F& F2) const {
// Determine whether to transpose F1
const Matrix3 Fca =
edge1_.i() == c_ ? F1.matrix() : F1.matrix().transpose();
// Determine whether to transpose F2
const Matrix3 Fcb =
edge2_.i() == c_ ? F2.matrix() : F2.matrix().transpose();
return {Fca, Fcb};
}
};
/**
* Binary factor in the context of Structure from Motion (SfM).
* It is used to transfer transfer corresponding points from two views to a
@ -30,89 +84,239 @@ namespace gtsam {
* the target view. Jacobians are done using numerical differentiation.
*/
template <typename F>
class TransferFactor : public NoiseModelFactorN<F, F> {
EdgeKey key1_, key2_; ///< the two EdgeKeys
std::vector<std::tuple<Point2, Point2, Point2>>
triplets_; ///< Point triplets
class TransferFactor : public NoiseModelFactorN<F, F>, public TransferEdges<F> {
public:
using Base = NoiseModelFactorN<F, F>;
using Triplet = std::tuple<Point2, Point2, Point2>;
protected:
std::vector<Triplet> triplets_; ///< Point triplets.
public:
/**
* @brief Constructor for a single triplet of points
*
* @note: batching all points for the same transfer will be much faster.
*
* @param key1 First EdgeKey specifying F1: (a, c) or (c, a).
* @param key2 Second EdgeKey specifying F2: (b, c) or (c, b).
* @param pa The point in the first view (a).
* @param pb The point in the second view (b).
* @param pc The point in the third (and transfer target) view (c).
* @param model An optional SharedNoiseModel that defines the noise model
* for this factor. Defaults to nullptr.
*/
TransferFactor(EdgeKey key1, EdgeKey key2, const Point2& pa, const Point2& pb,
const Point2& pc, const SharedNoiseModel& model = nullptr)
: NoiseModelFactorN<F, F>(model, key1, key2),
key1_(key1),
key2_(key2),
triplets_({std::make_tuple(pa, pb, pc)}) {}
/**
* @brief Constructor that accepts a vector of point triplets.
*
* @param key1 First EdgeKey specifying F1: (a, c) or (c, a).
* @param key2 Second EdgeKey specifying F2: (b, c) or (c, b).
* @param edge1 First EdgeKey specifying F1: (a, c) or (c, a).
* @param edge2 Second EdgeKey specifying F2: (b, c) or (c, b).
* @param triplets A vector of triplets containing (pa, pb, pc).
* @param model An optional SharedNoiseModel that defines the noise model
* for this factor. Defaults to nullptr.
*/
TransferFactor(
EdgeKey key1, EdgeKey key2,
const std::vector<std::tuple<Point2, Point2, Point2>>& triplets,
const SharedNoiseModel& model = nullptr)
: NoiseModelFactorN<F, F>(model, key1, key2),
key1_(key1),
key2_(key2),
TransferFactor(EdgeKey edge1, EdgeKey edge2,
const std::vector<Triplet>& triplets,
const SharedNoiseModel& model = nullptr)
: Base(model, edge1, edge2),
TransferEdges<F>(edge1, edge2),
triplets_(triplets) {}
// Create Matrix3 objects based on EdgeKey configurations
std::pair<Matrix3, Matrix3> getMatrices(const F& F1, const F& F2) const {
// Fill Fca and Fcb based on EdgeKey configurations
if (key1_.i() == key2_.i()) {
return {F1.matrix(), F2.matrix()};
} else if (key1_.i() == key2_.j()) {
return {F1.matrix(), F2.matrix().transpose()};
} else if (key1_.j() == key2_.i()) {
return {F1.matrix().transpose(), F2.matrix()};
} else if (key1_.j() == key2_.j()) {
return {F1.matrix().transpose(), F2.matrix().transpose()};
} else {
throw std::runtime_error(
"TransferFactor: invalid EdgeKey configuration.");
}
}
/// vector of errors returns 2*N vector
/// Vector of errors returns 2*N vector.
Vector evaluateError(const F& F1, const F& F2,
OptionalMatrixType H1 = nullptr,
OptionalMatrixType H2 = nullptr) const override {
std::function<Vector(const F&, const F&)> transfer = [&](const F& F1,
const F& F2) {
std::function<Vector(const F&, const F&)> errorFunction = [&](const F& f1,
const F& f2) {
Vector errors(2 * triplets_.size());
size_t idx = 0;
auto [Fca, Fcb] = getMatrices(F1, F2);
for (const auto& tuple : triplets_) {
const auto& [pa, pb, pc] = tuple;
Point2 transferredPoint = EpipolarTransfer(Fca, pa, Fcb, pb);
Vector2 error = transferredPoint - pc;
errors.segment<2>(idx) = error;
auto [Fca, Fcb] = this->getMatrices(f1, f2);
for (const auto& [pa, pb, pc] : triplets_) {
errors.segment<2>(idx) = EpipolarTransfer(Fca, pa, Fcb, pb) - pc;
idx += 2;
}
return errors;
};
if (H1) *H1 = numericalDerivative21<Vector, F, F>(transfer, F1, F2);
if (H2) *H2 = numericalDerivative22<Vector, F, F>(transfer, F1, F2);
return transfer(F1, F2);
if (H1) *H1 = numericalDerivative21(errorFunction, F1, F2);
if (H2) *H2 = numericalDerivative22(errorFunction, F1, F2);
return errorFunction(F1, F2);
}
};
/**
* @class EssentialTransferFactor
* @brief Transfers points between views using essential matrices with a shared
* calibration.
*
* This factor is templated on the calibration class K and extends
* the TransferFactor for EssentialMatrices. It involves two essential matrices
* and a shared calibration object (K). The evaluateError function calibrates
* the image points, calls the base class's transfer method, and computes the
* error using bulk numerical differentiation.
*/
template <typename K>
class EssentialTransferFactor : public TransferFactor<EssentialMatrix> {
using EM = EssentialMatrix;
using Triplet = std::tuple<Point2, Point2, Point2>;
std::shared_ptr<K> calibration_; ///< Shared pointer to calibration object
public:
using Base = TransferFactor<EM>;
using This = EssentialTransferFactor<K>;
using shared_ptr = std::shared_ptr<This>;
/**
* @brief Constructor that accepts a vector of point triplets and a shared
* calibration.
*
* @param edge1 First EdgeKey specifying E1: (a, c) or (c, a)
* @param edge2 Second EdgeKey specifying E2: (b, c) or (c, b)
* @param triplets A vector of triplets containing (pa, pb, pc)
* @param calibration Shared pointer to calibration object
* @param model An optional SharedNoiseModel
*/
EssentialTransferFactor(EdgeKey edge1, EdgeKey edge2,
const std::vector<Triplet>& triplets,
const std::shared_ptr<K>& calibration,
const SharedNoiseModel& model = nullptr)
: Base(edge1, edge2, triplets, model), calibration_(calibration) {}
/// Transfer points pa and pb to view c and evaluate error.
Vector2 TransferError(const Matrix3& Eca, const Point2& pa,
const Matrix3& Ecb, const Point2& pb,
const Point2& pc) const {
const Point2 pA = calibration_->calibrate(pa);
const Point2 pB = calibration_->calibrate(pb);
const Point2 pC = EpipolarTransfer(Eca, pA, Ecb, pB);
return calibration_->uncalibrate(pC) - pc;
}
/// Evaluate error function
Vector evaluateError(const EM& E1, const EM& E2,
OptionalMatrixType H1 = nullptr,
OptionalMatrixType H2 = nullptr) const override {
std::function<Vector(const EM&, const EM&)> errorFunction =
[&](const EM& e1, const EM& e2) {
Vector errors(2 * this->triplets_.size());
size_t idx = 0;
auto [Eca, Ecb] = this->getMatrices(e1, e2);
for (const auto& [pa, pb, pc] : this->triplets_) {
errors.segment<2>(idx) = TransferError(Eca, pa, Ecb, pb, pc);
idx += 2;
}
return errors;
};
// Compute error
Vector errors = errorFunction(E1, E2);
// Compute Jacobians if requested
if (H1) *H1 = numericalDerivative21(errorFunction, E1, E2);
if (H2) *H2 = numericalDerivative22(errorFunction, E1, E2);
return errors;
}
};
/**
* @class EssentialTransferFactorK
* @brief Transfers points between views using essential matrices, optimizes for
* calibrations of the views, as well. Note that the EssentialMatrixFactor4 does
* something similar but without transfer.
*
* @note Derives calibration keys from edges, and uses symbol 'k'.
*
* This factor is templated on the calibration class K and extends
* the TransferFactor for EssentialMatrices. It involves two essential matrices
* and three calibration objects (Ka, Kb, Kc). The evaluateError
* function calibrates the image points, calls the base class's transfer method,
* and computes the error using bulk numerical differentiation.
*/
template <typename K>
class EssentialTransferFactorK
: public NoiseModelFactorN<EssentialMatrix, EssentialMatrix, K, K, K>,
TransferEdges<EssentialMatrix> {
using EM = EssentialMatrix;
using Triplet = std::tuple<Point2, Point2, Point2>;
std::vector<Triplet> triplets_; ///< Point triplets
public:
using Base = NoiseModelFactorN<EM, EM, K, K, K>;
using This = EssentialTransferFactorK<K>;
using shared_ptr = std::shared_ptr<This>;
/**
* @brief Constructor that accepts a vector of point triplets.
*
* @note Calibrations are assumed all different, keys are derived from edges.
*
* @param edge1 First EdgeKey specifying E1: (a, c) or (c, a)
* @param edge2 Second EdgeKey specifying E2: (b, c) or (c, b)
* @param triplets A vector of triplets containing (pa, pb, pc)
* @param model An optional SharedNoiseModel
*/
EssentialTransferFactorK(EdgeKey edge1, EdgeKey edge2,
const std::vector<Triplet>& triplets,
const SharedNoiseModel& model = nullptr)
: Base(model, edge1, edge2,
Symbol('k', ViewA(edge1, edge2)), // calibration key for view a
Symbol('k', ViewB(edge1, edge2)), // calibration key for view b
Symbol('k', ViewC(edge1, edge2))), // calibration key for target c
TransferEdges<EM>(edge1, edge2),
triplets_(triplets) {}
/**
* @brief Constructor that accepts a vector of point triplets.
*
* @note Calibrations are assumed all same, using given key `keyK`.
*
* @param edge1 First EdgeKey specifying E1: (a, c) or (c, a)
* @param edge2 Second EdgeKey specifying E2: (b, c) or (c, b)
* @param keyK Calibration key for all views.
* @param triplets A vector of triplets containing (pa, pb, pc)
* @param model An optional SharedNoiseModel
*/
EssentialTransferFactorK(EdgeKey edge1, EdgeKey edge2, Key keyK,
const std::vector<Triplet>& triplets,
const SharedNoiseModel& model = nullptr)
: Base(model, edge1, edge2, keyK, keyK, keyK),
TransferEdges<EM>(edge1, edge2),
triplets_(triplets) {}
/// Transfer points pa and pb to view c and evaluate error.
Vector2 TransferError(const Matrix3& Eca, const K& Ka, const Point2& pa,
const Matrix3& Ecb, const K& Kb, const Point2& pb,
const K& Kc, const Point2& pc) const {
const Point2 pA = Ka.calibrate(pa);
const Point2 pB = Kb.calibrate(pb);
const Point2 pC = EpipolarTransfer(Eca, pA, Ecb, pB);
return Kc.uncalibrate(pC) - pc;
}
/// Evaluate error function
Vector evaluateError(const EM& E1, const EM& E2, const K& Ka, const K& Kb,
const K& Kc, OptionalMatrixType H1 = nullptr,
OptionalMatrixType H2 = nullptr,
OptionalMatrixType H3 = nullptr,
OptionalMatrixType H4 = nullptr,
OptionalMatrixType H5 = nullptr) const override {
std::function<Vector(const EM&, const EM&, const K&, const K&, const K&)>
errorFunction = [&](const EM& e1, const EM& e2, const K& kA,
const K& kB, const K& kC) {
Vector errors(2 * triplets_.size());
size_t idx = 0;
auto [Eca, Ecb] = this->getMatrices(e1, e2);
for (const auto& [pa, pb, pc] : triplets_) {
errors.segment<2>(idx) =
TransferError(Eca, kA, pa, Ecb, kB, pb, kC, pc);
idx += 2;
}
return errors;
};
// Compute error
Vector errors = errorFunction(E1, E2, Ka, Kb, Kc);
// Compute Jacobians if requested
if (H1) *H1 = numericalDerivative51(errorFunction, E1, E2, Ka, Kb, Kc);
if (H2) *H2 = numericalDerivative52(errorFunction, E1, E2, Ka, Kb, Kc);
if (H3) *H3 = numericalDerivative53(errorFunction, E1, E2, Ka, Kb, Kc);
if (H4) *H4 = numericalDerivative54(errorFunction, E1, E2, Ka, Kb, Kc);
if (H5) *H5 = numericalDerivative55(errorFunction, E1, E2, Ka, Kb, Kc);
return errors;
}
/// Return the dimension of the factor
size_t dim() const override { return 2 * triplets_.size(); }
};
} // namespace gtsam

30
gtsam/sfm/sfm.i
View File

@ -75,6 +75,36 @@ bool writeBAL(string filename, gtsam::SfmData& data);
gtsam::Values initialCamerasEstimate(const gtsam::SfmData& db);
gtsam::Values initialCamerasAndPointsEstimate(const gtsam::SfmData& db);
#include <gtsam/sfm/TransferFactor.h>
#include <gtsam/geometry/FundamentalMatrix.h>
template <F = {gtsam::SimpleFundamentalMatrix, gtsam::FundamentalMatrix}>
virtual class TransferFactor : gtsam::NoiseModelFactor {
TransferFactor(gtsam::EdgeKey edge1, gtsam::EdgeKey edge2,
const std::vector<std::tuple<gtsam::Point2, gtsam::Point2, gtsam::Point2>>& triplets,
const gtsam::noiseModel::Base* model = nullptr);
};
#include <gtsam/geometry/Cal3_S2.h>
#include <gtsam/geometry/Cal3f.h>
#include <gtsam/geometry/Cal3Bundler.h>
template <K = {gtsam::Cal3_S2, gtsam::Cal3f, gtsam::Cal3Bundler}>
virtual class EssentialTransferFactor : gtsam::NoiseModelFactor {
EssentialTransferFactor(gtsam::EdgeKey edge1, gtsam::EdgeKey edge2,
const std::vector<std::tuple<gtsam::Point2, gtsam::Point2, gtsam::Point2>>& triplets,
const K* calibration,
const gtsam::noiseModel::Base* model = nullptr);
};
template <K = {gtsam::Cal3_S2, gtsam::Cal3f, gtsam::Cal3Bundler}>
virtual class EssentialTransferFactorK : gtsam::NoiseModelFactor {
EssentialTransferFactorK(gtsam::EdgeKey edge1, gtsam::EdgeKey edge2,
const std::vector<std::tuple<gtsam::Point2, gtsam::Point2, gtsam::Point2>>& triplets,
const gtsam::noiseModel::Base* model = nullptr);
EssentialTransferFactorK(gtsam::EdgeKey edge1, gtsam::EdgeKey edge2, size_t keyK,
const std::vector<std::tuple<gtsam::Point2, gtsam::Point2, gtsam::Point2>>& triplets,
const gtsam::noiseModel::Base* model = nullptr);
};
#include <gtsam/sfm/ShonanFactor.h>
virtual class ShonanFactor3 : gtsam::NoiseModelFactor {

133
gtsam/sfm/tests/testTransferFactor.cpp
View File

@ -1,19 +1,23 @@
/*
* @file testTransferFactor.cpp
* @brief Test TransferFactor class
* @author Your Name
* @date October 23, 2024
* @brief Test TransferFactor classes
* @author Frank Dellaert
* @date October 2024
*/
#include <CppUnitLite/TestHarness.h>
#include <gtsam/geometry/Cal3_S2.h>
#include <gtsam/geometry/SimpleCamera.h>
#include <gtsam/nonlinear/factorTesting.h>
#include <gtsam/sfm/TransferFactor.h>
#include <memory>
using namespace gtsam;
using symbol_shorthand::K;
//*************************************************************************
/// Generate three cameras on a circle, looking in
/// Generate three cameras on a circle, looking inwards
std::array<Pose3, 3> generateCameraPoses() {
std::array<Pose3, 3> cameraPoses;
const double radius = 1.0;
@ -48,8 +52,12 @@ std::array<Pose3, 3> cameraPoses = generateCameraPoses();
auto triplet = generateTripleF(cameraPoses);
double focalLength = 1000;
Point2 principalPoint(640 / 2, 480 / 2);
const Cal3_S2 K(focalLength, focalLength, 0.0, //
principalPoint.x(), principalPoint.y());
const Cal3_S2 cal(focalLength, focalLength, 0.0, //
principalPoint.x(), principalPoint.y());
// Create cameras
auto f = [](const Pose3& pose) { return PinholeCamera<Cal3_S2>(pose, cal); };
std::array<PinholeCamera<Cal3_S2>, 3> cameras = {
f(cameraPoses[0]), f(cameraPoses[1]), f(cameraPoses[2])};
} // namespace fixture
//*************************************************************************
@ -71,20 +79,17 @@ TEST(TransferFactor, Jacobians) {
// Now project a point into the three cameras
const Point3 P(0.1, 0.2, 0.3);
std::array<Point2, 3> p;
for (size_t i = 0; i < 3; ++i) {
// Project the point into each camera
PinholeCameraCal3_S2 camera(cameraPoses[i], K);
p[i] = camera.project(P);
p[i] = cameras[i].project(P);
}
// Create a TransferFactor
EdgeKey key01(0, 1), key12(1, 2), key20(2, 0);
TransferFactor<SimpleFundamentalMatrix> //
factor0{key01, key20, p[1], p[2], p[0]},
factor1{key12, key01, p[2], p[0], p[1]},
factor2{key20, key12, p[0], p[1], p[2]};
factor0{key01, key20, {{p[1], p[2], p[0]}}},
factor1{key12, key01, {{p[2], p[0], p[1]}}},
factor2{key20, key12, {{p[0], p[1], p[2]}}};
// Create Values with edge keys
Values values;
@ -107,19 +112,14 @@ TEST(TransferFactor, MultipleTuples) {
// Now project multiple points into the three cameras
const size_t numPoints = 5; // Number of points to test
std::vector<Point3> points3D;
std::vector<std::array<Point2, 3>> projectedPoints;
// Generate random 3D points and project them
for (size_t n = 0; n < numPoints; ++n) {
Point3 P(0.1 * n, 0.2 * n, 0.3 + 0.1 * n);
points3D.push_back(P);
std::array<Point2, 3> p;
for (size_t i = 0; i < 3; ++i) {
// Project the point into each camera
PinholeCameraCal3_S2 camera(cameraPoses[i], K);
p[i] = camera.project(P);
p[i] = cameras[i].project(P);
}
projectedPoints.push_back(p);
}
@ -153,9 +153,102 @@ TEST(TransferFactor, MultipleTuples) {
EXPECT_CORRECT_FACTOR_JACOBIANS(factor, values, 1e-5, 1e-7);
}
//*************************************************************************
// Test for EssentialTransferFactorK
TEST(EssentialTransferFactor, Jacobians) {
using namespace fixture;
// Create EssentialMatrices between cameras
EssentialMatrix E01 =
EssentialMatrix::FromPose3(cameraPoses[0].between(cameraPoses[1]));
EssentialMatrix E02 =
EssentialMatrix::FromPose3(cameraPoses[0].between(cameraPoses[2]));
// Project a point into the three cameras
const Point3 P(0.1, 0.2, 0.3);
std::array<Point2, 3> p;
for (size_t i = 0; i < 3; ++i) {
p[i] = cameras[i].project(P);
}
// Create EdgeKeys
EdgeKey key01(0, 1);
EdgeKey key02(0, 2);
// Create an EssentialTransferFactor
auto sharedCal = std::make_shared<Cal3_S2>(cal);
EssentialTransferFactor<Cal3_S2> factor(key01, key02, {{p[1], p[2], p[0]}},
sharedCal);
// Create Values and insert variables
Values values;
values.insert(key01, E01); // Essential matrix between views 0 and 1
values.insert(key02, E02); // Essential matrix between views 0 and 2
// Check error
Matrix H1, H2, H3, H4, H5;
Vector error = factor.evaluateError(E01, E02, //
&H1, &H2);
EXPECT(H1.rows() == 2 && H1.cols() == 5)
EXPECT(H2.rows() == 2 && H2.cols() == 5)
EXPECT(assert_equal(Vector::Zero(2), error, 1e-9))
// Check Jacobians
EXPECT_CORRECT_FACTOR_JACOBIANS(factor, values, 1e-5, 1e-7);
}
//*************************************************************************
// Test for EssentialTransferFactorK
TEST(EssentialTransferFactorK, Jacobians) {
using namespace fixture;
// Create EssentialMatrices between cameras
EssentialMatrix E01 =
EssentialMatrix::FromPose3(cameraPoses[0].between(cameraPoses[1]));
EssentialMatrix E02 =
EssentialMatrix::FromPose3(cameraPoses[0].between(cameraPoses[2]));
// Project a point into the three cameras
const Point3 P(0.1, 0.2, 0.3);
std::array<Point2, 3> p;
for (size_t i = 0; i < 3; ++i) {
p[i] = cameras[i].project(P);
}
// Create EdgeKeys
EdgeKey key01(0, 1);
EdgeKey key02(0, 2);
// Create an EssentialTransferFactorK
EssentialTransferFactorK<Cal3_S2> factor(key01, key02, {{p[1], p[2], p[0]}});
// Create Values and insert variables
Values values;
values.insert(key01, E01); // Essential matrix between views 0 and 1
values.insert(key02, E02); // Essential matrix between views 0 and 2
values.insert(K(1), cal); // Calibration for view A (view 1)
values.insert(K(2), cal); // Calibration for view B (view 2)
values.insert(K(0), cal); // Calibration for view C (view 0)
// Check error
Matrix H1, H2, H3, H4, H5;
Vector error = factor.evaluateError(E01, E02, //
cal, cal, cal, //
&H1, &H2, &H3, &H4, &H5);
EXPECT(H1.rows() == 2 && H1.cols() == 5)
EXPECT(H2.rows() == 2 && H2.cols() == 5)
EXPECT(H3.rows() == 2 && H3.cols() == 5)
EXPECT(H4.rows() == 2 && H4.cols() == 5)
EXPECT(H5.rows() == 2 && H5.cols() == 5)
EXPECT(assert_equal(Vector::Zero(2), error, 1e-9))
// Check Jacobians
EXPECT_CORRECT_FACTOR_JACOBIANS(factor, values, 1e-5, 1e-7);
}
//*************************************************************************
int main() {
TestResult tr;
return TestRegistry::runAllTests(tr);
}
//*************************************************************************
//*************************************************************************

153
gtsam/slam/EssentialMatrixFactor.h
View File

@ -38,7 +38,6 @@ class EssentialMatrixFactor : public NoiseModelFactorN<EssentialMatrix> {
typedef EssentialMatrixFactor This;
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
@ -93,8 +92,8 @@ class EssentialMatrixFactor : public NoiseModelFactorN<EssentialMatrix> {
}
/// vector of errors returns 1D vector
Vector evaluateError(
const EssentialMatrix& E, OptionalMatrixType H) const override {
Vector evaluateError(const EssentialMatrix& E,
OptionalMatrixType H) const override {
Vector error(1);
error << E.error(vA_, vB_, H);
return error;
@ -118,7 +117,6 @@ class EssentialMatrixFactor2
typedef EssentialMatrixFactor2 This;
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
@ -178,9 +176,9 @@ class EssentialMatrixFactor2
* @param E essential matrix
* @param d inverse depth d
*/
Vector evaluateError(
const EssentialMatrix& E, const double& d,
OptionalMatrixType DE, OptionalMatrixType Dd) const override {
Vector evaluateError(const EssentialMatrix& E, const double& d,
OptionalMatrixType DE,
OptionalMatrixType Dd) const override {
// We have point x,y in image 1
// Given a depth Z, the corresponding 3D point P1 = Z*(x,y,1) = (x,y,1)/d
// We then convert to second camera by P2 = 1R2'*(P1-1T2)
@ -241,7 +239,6 @@ class EssentialMatrixFactor3 : public EssentialMatrixFactor2 {
Rot3 cRb_; ///< Rotation from body to camera frame
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
@ -292,9 +289,9 @@ class EssentialMatrixFactor3 : public EssentialMatrixFactor2 {
* @param E essential matrix
* @param d inverse depth d
*/
Vector evaluateError(
const EssentialMatrix& E, const double& d,
OptionalMatrixType DE, OptionalMatrixType Dd) const override {
Vector evaluateError(const EssentialMatrix& E, const double& d,
OptionalMatrixType DE,
OptionalMatrixType Dd) const override {
if (!DE) {
// Convert E from body to camera frame
EssentialMatrix cameraE = cRb_ * E;
@ -304,8 +301,9 @@ class EssentialMatrixFactor3 : public EssentialMatrixFactor2 {
// Version with derivatives
Matrix D_e_cameraE, D_cameraE_E; // 2*5, 5*5
EssentialMatrix cameraE = E.rotate(cRb_, D_cameraE_E);
// Using the pointer version of evaluateError since the Base class (EssentialMatrixFactor2)
// does not have the matrix reference version of evaluateError
// Using the pointer version of evaluateError since the Base class
// (EssentialMatrixFactor2) does not have the matrix reference version of
// evaluateError
Vector e = Base::evaluateError(cameraE, d, &D_e_cameraE, Dd);
*DE = D_e_cameraE * D_cameraE_E; // (2*5) * (5*5)
return e;
@ -327,7 +325,7 @@ class EssentialMatrixFactor3 : public EssentialMatrixFactor2 {
* Even with a prior, we can only optimize 2 DoF in the calibration. So the
* prior should have a noise model with very low sigma in the remaining
* dimensions. This has been tested to work on Cal3_S2. With Cal3Bundler, it
* works only with a strong prior (low sigma noisemodel) on all degrees of
* works only with a strong prior (low sigma noise model) on all degrees of
* freedom.
*/
template <class CALIBRATION>
@ -343,13 +341,12 @@ class EssentialMatrixFactor4
typedef Eigen::Matrix<double, 2, DimK> JacobianCalibration;
public:
// Provide access to the Matrix& version of evaluateError:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
/**
* Constructor
* @param keyE Essential Matrix (from camera B to A) variable key
* @param keyE Essential Matrix aEb variable key
* @param keyK Calibration variable key (common for both cameras)
* @param pA point in first camera, in pixel coordinates
* @param pB point in second camera, in pixel coordinates
@ -357,7 +354,7 @@ class EssentialMatrixFactor4
* coordinates
*/
EssentialMatrixFactor4(Key keyE, Key keyK, const Point2& pA, const Point2& pB,
const SharedNoiseModel& model)
const SharedNoiseModel& model = nullptr)
: Base(model, keyE, keyK), pA_(pA), pB_(pB) {}
/// @return a deep copy of this factor
@ -385,32 +382,32 @@ class EssentialMatrixFactor4
* @param H2 optional jacobian of error w.r.t K
* @return * Vector 1D vector of algebraic error
*/
Vector evaluateError(
const EssentialMatrix& E, const CALIBRATION& K,
OptionalMatrixType H1, OptionalMatrixType H2) const override {
Vector evaluateError(const EssentialMatrix& E, const CALIBRATION& K,
OptionalMatrixType HE,
OptionalMatrixType HK) const override {
// converting from pixel coordinates to normalized coordinates cA and cB
JacobianCalibration cA_H_K; // dcA/dK
JacobianCalibration cB_H_K; // dcB/dK
Point2 cA = K.calibrate(pA_, H2 ? &cA_H_K : 0, OptionalNone);
Point2 cB = K.calibrate(pB_, H2 ? &cB_H_K : 0, OptionalNone);
Point2 cA = K.calibrate(pA_, HK ? &cA_H_K : 0, OptionalNone);
Point2 cB = K.calibrate(pB_, HK ? &cB_H_K : 0, OptionalNone);
// convert to homogeneous coordinates
Vector3 vA = EssentialMatrix::Homogeneous(cA);
Vector3 vB = EssentialMatrix::Homogeneous(cB);
if (H2) {
if (HK) {
// compute the jacobian of error w.r.t K
// error function f = vA.T * E * vB
// H2 = df/dK = vB.T * E.T * dvA/dK + vA.T * E * dvB/dK
// where dvA/dK = dvA/dcA * dcA/dK, dVB/dK = dvB/dcB * dcB/dK
// and dvA/dcA = dvB/dcB = [[1, 0], [0, 1], [0, 0]]
*H2 = vB.transpose() * E.matrix().transpose().leftCols<2>() * cA_H_K +
*HK = vB.transpose() * E.matrix().transpose().leftCols<2>() * cA_H_K +
vA.transpose() * E.matrix().leftCols<2>() * cB_H_K;
}
Vector error(1);
error << E.error(vA, vB, H1);
error << E.error(vA, vB, HE);
return error;
}
@ -420,4 +417,108 @@ class EssentialMatrixFactor4
};
// EssentialMatrixFactor4
/**
* Binary factor that optimizes for E and two calibrations Ka and Kb using the
* algebraic epipolar error (Ka^-1 pA)'E (Kb^-1 pB). The calibrations are
* assumed different for the two images, but if you use the same key for Ka and
* Kb, the sum of the two K Jacobians equals that of the K Jacobian for
* EssentialMatrix4. If you know there is a single global calibration, use
* that factor instead.
*
* Note: see the comment about priors from EssentialMatrixFactor4: even stronger
* caveats about having priors on calibration apply here.
*/
template <class CALIBRATION>
class EssentialMatrixFactor5
: public NoiseModelFactorN<EssentialMatrix, CALIBRATION, CALIBRATION> {
private:
Point2 pA_, pB_; ///< points in pixel coordinates
typedef NoiseModelFactorN<EssentialMatrix, CALIBRATION, CALIBRATION> Base;
typedef EssentialMatrixFactor5 This;
static constexpr int DimK = FixedDimension<CALIBRATION>::value;
typedef Eigen::Matrix<double, 2, DimK> JacobianCalibration;
public:
// Provide access to the Matrix& version of evaluateError:
using Base::evaluateError;
/**
* Constructor
* @param keyE Essential Matrix aEb variable key
* @param keyKa Calibration variable key for camera A
* @param keyKb Calibration variable key for camera B
* @param pA point in first camera, in pixel coordinates
* @param pB point in second camera, in pixel coordinates
* @param model noise model is about dot product in ideal, homogeneous
* coordinates
*/
EssentialMatrixFactor5(Key keyE, Key keyKa, Key keyKb, const Point2& pA,
const Point2& pB,
const SharedNoiseModel& model = nullptr)
: Base(model, keyE, keyKa, keyKb), pA_(pA), pB_(pB) {}
/// @return a deep copy of this factor
gtsam::NonlinearFactor::shared_ptr clone() const override {
return std::static_pointer_cast<gtsam::NonlinearFactor>(
gtsam::NonlinearFactor::shared_ptr(new This(*this)));
}
/// print
void print(
const std::string& s = "",
const KeyFormatter& keyFormatter = DefaultKeyFormatter) const override {
Base::print(s);
std::cout << " EssentialMatrixFactor5 with measurements\n ("
<< pA_.transpose() << ")' and (" << pB_.transpose() << ")'"
<< std::endl;
}
/**
* @brief Calculate the algebraic epipolar error pA' (Ka^-1)' E Kb pB.
*
* @param E essential matrix for key keyE
* @param Ka calibration for camera A for key keyKa
* @param Kb calibration for camera B for key keyKb
* @param H1 optional jacobian of error w.r.t E
* @param H2 optional jacobian of error w.r.t Ka
* @param H3 optional jacobian of error w.r.t Kb
* @return * Vector 1D vector of algebraic error
*/
Vector evaluateError(const EssentialMatrix& E, const CALIBRATION& Ka,
const CALIBRATION& Kb, OptionalMatrixType HE,
OptionalMatrixType HKa,
OptionalMatrixType HKb) const override {
// converting from pixel coordinates to normalized coordinates cA and cB
JacobianCalibration cA_H_Ka; // dcA/dKa
JacobianCalibration cB_H_Kb; // dcB/dKb
Point2 cA = Ka.calibrate(pA_, HKa ? &cA_H_Ka : 0, OptionalNone);
Point2 cB = Kb.calibrate(pB_, HKb ? &cB_H_Kb : 0, OptionalNone);
// Convert to homogeneous coordinates.
Vector3 vA = EssentialMatrix::Homogeneous(cA);
Vector3 vB = EssentialMatrix::Homogeneous(cB);
if (HKa) {
// Compute the jacobian of error w.r.t Ka.
*HKa = vB.transpose() * E.matrix().transpose().leftCols<2>() * cA_H_Ka;
}
if (HKb) {
// Compute the jacobian of error w.r.t Kb.
*HKb = vA.transpose() * E.matrix().leftCols<2>() * cB_H_Kb;
}
Vector error(1);
error << E.error(vA, vB, HE);
return error;
}
public:
GTSAM_MAKE_ALIGNED_OPERATOR_NEW
};
// EssentialMatrixFactor5
} // namespace gtsam

50
gtsam/slam/slam.i
View File

@ -107,7 +107,7 @@ typedef gtsam::GeneralSFMFactor<gtsam::PinholePose<gtsam::Cal3Unified>,
gtsam::Point3>
GeneralSFMFactorPoseCal3Unified;
template <CALIBRATION = {gtsam::Cal3_S2, gtsam::Cal3DS2, gtsam::Cal3Bundler,
template <CALIBRATION = {gtsam::Cal3_S2, gtsam::Cal3DS2, gtsam::Cal3f, gtsam::Cal3Bundler,
gtsam::Cal3Fisheye, gtsam::Cal3Unified}>
virtual class GeneralSFMFactor2 : gtsam::NoiseModelFactor {
GeneralSFMFactor2(const gtsam::Point2& measured,
@ -221,15 +221,55 @@ typedef gtsam::PoseRotationPrior<gtsam::Pose3> PoseRotationPrior3D;
#include <gtsam/slam/EssentialMatrixFactor.h>
virtual class EssentialMatrixFactor : gtsam::NoiseModelFactor {
EssentialMatrixFactor(size_t key, const gtsam::Point2& pA,
const gtsam::Point2& pB,
const gtsam::noiseModel::Base* noiseModel);
EssentialMatrixFactor(size_t key,
const gtsam::Point2& pA, const gtsam::Point2& pB,
const gtsam::noiseModel::Base* model);
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
bool equals(const gtsam::EssentialMatrixFactor& other, double tol) const;
gtsam::Vector evaluateError(const gtsam::EssentialMatrix& E) const;
};
virtual class EssentialMatrixFactor2 : gtsam::NoiseModelFactor {
EssentialMatrixFactor2(size_t key1, size_t key2,
const gtsam::Point2& pA, const gtsam::Point2& pB,
const gtsam::noiseModel::Base* model);
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
gtsam::Vector evaluateError(const gtsam::EssentialMatrix& E, double d) const;
};
virtual class EssentialMatrixFactor3 : gtsam::EssentialMatrixFactor2 {
EssentialMatrixFactor3(size_t key1, size_t key2,
const gtsam::Point2& pA, const gtsam::Point2& pB,
const gtsam::Rot3& cRb, const gtsam::noiseModel::Base* model);
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
gtsam::Vector evaluateError(const gtsam::EssentialMatrix& E, double d) const;
};
template <CALIBRATION = {gtsam::Cal3_S2, gtsam::Cal3DS2, gtsam::Cal3f, gtsam::Cal3Bundler,
gtsam::Cal3Fisheye, gtsam::Cal3Unified}>
virtual class EssentialMatrixFactor4 : gtsam::NoiseModelFactor {
EssentialMatrixFactor4(size_t keyE, size_t keyK,
const gtsam::Point2& pA, const gtsam::Point2& pB,
const gtsam::noiseModel::Base* model = nullptr);
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
gtsam::Vector evaluateError(const gtsam::EssentialMatrix& E, const CALIBRATION& K) const;
};
template <CALIBRATION = {gtsam::Cal3_S2, gtsam::Cal3DS2, gtsam::Cal3f, gtsam::Cal3Bundler,
gtsam::Cal3Fisheye, gtsam::Cal3Unified}>
virtual class EssentialMatrixFactor5 : gtsam::NoiseModelFactor {
EssentialMatrixFactor5(size_t keyE, size_t keyKa, size_t keyKb,
const gtsam::Point2& pA, const gtsam::Point2& pB,
const gtsam::noiseModel::Base* model = nullptr);
void print(string s = "", const gtsam::KeyFormatter& keyFormatter =
gtsam::DefaultKeyFormatter) const;
gtsam::Vector evaluateError(const gtsam::EssentialMatrix& E,
const CALIBRATION& Ka, const CALIBRATION& Kb) const;
};
#include <gtsam/slam/EssentialMatrixConstraint.h>
virtual class EssentialMatrixConstraint : gtsam::NoiseModelFactor {
EssentialMatrixConstraint(size_t key1, size_t key2, const gtsam::EssentialMatrix &measuredE,

70
gtsam/slam/tests/testEssentialMatrixFactor.cpp
View File

@ -14,8 +14,8 @@
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
#include <gtsam/nonlinear/expressionTesting.h>
#include <gtsam/nonlinear/factorTesting.h>
#include <gtsam/slam/EssentialMatrixFactor.h>
#include <gtsam/sfm/SfmData.h>
#include <gtsam/slam/EssentialMatrixFactor.h>
#include <gtsam/slam/dataset.h>
using namespace std::placeholders;
@ -101,7 +101,8 @@ TEST(EssentialMatrixFactor, ExpressionFactor) {
Key key(1);
for (size_t i = 0; i < 5; i++) {
std::function<double(const EssentialMatrix &, OptionalJacobian<1, 5>)> f =
std::bind(&EssentialMatrix::error, std::placeholders::_1, vA(i), vB(i), std::placeholders::_2);
std::bind(&EssentialMatrix::error, std::placeholders::_1, vA(i), vB(i),
std::placeholders::_2);
Expression<EssentialMatrix> E_(key); // leaf expression
Expression<double> expr(f, E_); // unary expression
@ -116,8 +117,8 @@ TEST(EssentialMatrixFactor, ExpressionFactor) {
// Check evaluation
Vector expected(1);
expected << 0;
vector<Matrix> Hactual(1);
Vector actual = factor.unwhitenedError(values, Hactual);
vector<Matrix> actualH(1);
Vector actual = factor.unwhitenedError(values, actualH);
EXPECT(assert_equal(expected, actual, 1e-7));
}
}
@ -127,10 +128,11 @@ TEST(EssentialMatrixFactor, ExpressionFactorRotationOnly) {
Key key(1);
for (size_t i = 0; i < 5; i++) {
std::function<double(const EssentialMatrix &, OptionalJacobian<1, 5>)> f =
std::bind(&EssentialMatrix::error, std::placeholders::_1, vA(i), vB(i), std::placeholders::_2);
std::bind(&EssentialMatrix::error, std::placeholders::_1, vA(i), vB(i),
std::placeholders::_2);
std::function<EssentialMatrix(const Rot3 &, const Unit3 &,
OptionalJacobian<5, 3>,
OptionalJacobian<5, 2>)>
OptionalJacobian<5, 3>,
OptionalJacobian<5, 2>)>
g;
Expression<Rot3> R_(key);
Expression<Unit3> d_(trueDirection);
@ -149,8 +151,8 @@ TEST(EssentialMatrixFactor, ExpressionFactorRotationOnly) {
// Check evaluation
Vector expected(1);
expected << 0;
vector<Matrix> Hactual(1);
Vector actual = factor.unwhitenedError(values, Hactual);
vector<Matrix> actualH(1);
Vector actual = factor.unwhitenedError(values, actualH);
EXPECT(assert_equal(expected, actual, 1e-7));
}
}
@ -211,9 +213,9 @@ TEST(EssentialMatrixFactor2, factor) {
const Point2 pi = PinholeBase::Project(P2);
Point2 expected(pi - pB(i));
Matrix Hactual1, Hactual2;
Matrix actualH1, actualH2;
double d(baseline / P1.z());
Vector actual = factor.evaluateError(trueE, d, Hactual1, Hactual2);
Vector actual = factor.evaluateError(trueE, d, actualH1, actualH2);
EXPECT(assert_equal(expected, actual, 1e-7));
Values val;
@ -276,9 +278,9 @@ TEST(EssentialMatrixFactor3, factor) {
const Point2 pi = camera2.project(P1);
Point2 expected(pi - pB(i));
Matrix Hactual1, Hactual2;
Matrix actualH1, actualH2;
double d(baseline / P1.z());
Vector actual = factor.evaluateError(bodyE, d, Hactual1, Hactual2);
Vector actual = factor.evaluateError(bodyE, d, actualH1, actualH2);
EXPECT(assert_equal(expected, actual, 1e-7));
Values val;
@ -529,6 +531,48 @@ TEST(EssentialMatrixFactor4, minimizationWithStrongCal3BundlerPrior) {
1e-6);
}
//*************************************************************************
TEST(EssentialMatrixFactor5, factor) {
Key keyE(1), keyKa(2), keyKb(3);
for (size_t i = 0; i < 5; i++) {
EssentialMatrixFactor5<Cal3_S2> factor(keyE, keyKa, keyKb, pA(i), pB(i),
model1);
// Check evaluation
Vector1 expected;
expected << 0;
Vector actual = factor.evaluateError(trueE, trueK, trueK);
EXPECT(assert_equal(expected, actual, 1e-7));
Values truth;
truth.insert(keyE, trueE);
truth.insert(keyKa, trueK);
truth.insert(keyKb, trueK);
EXPECT_CORRECT_FACTOR_JACOBIANS(factor, truth, 1e-6, 1e-7);
}
}
//*************************************************************************
// Test that if we use the same keys for Ka and Kb the sum of the two K
// Jacobians equals that of the single K Jacobian for EssentialMatrix4
TEST(EssentialMatrixFactor5, SameKeys) {
Key keyE(1), keyK(2);
for (size_t i = 0; i < 5; i++) {
EssentialMatrixFactor4<Cal3_S2> factor4(keyE, keyK, pA(i), pB(i), model1);
EssentialMatrixFactor5<Cal3_S2> factor5(keyE, keyK, keyK, pA(i), pB(i),
model1);
Values truth;
truth.insert(keyE, trueE);
truth.insert(keyK, trueK);
// Check Jacobians
Matrix H0, H1, H2;
factor4.evaluateError(trueE, trueK, nullptr, &H0);
factor5.evaluateError(trueE, trueK, trueK, nullptr, &H1, &H2);
EXPECT(assert_equal(H0, H1 + H2, 1e-9));
}
}
} // namespace example1
//*************************************************************************

5
python/CMakeLists.txt
View File

@ -156,6 +156,11 @@ foreach(test_file ${GTSAM_PYTHON_TEST_FILES})
get_filename_component(test_file_name ${test_file} NAME)
configure_file(${test_file} "${GTSAM_MODULE_PATH}/tests/${test_file_name}" COPYONLY)
endforeach()
file(GLOB GTSAM_PYTHON_TEST_FILES "${CMAKE_CURRENT_SOURCE_DIR}/gtsam/examples/*.py")
foreach(test_file ${GTSAM_PYTHON_TEST_FILES})
get_filename_component(test_file_name ${test_file} NAME)
configure_file(${test_file} "${GTSAM_MODULE_PATH}/tests/${test_file_name}" COPYONLY)
endforeach()
file(GLOB GTSAM_PYTHON_UTIL_FILES "${CMAKE_CURRENT_SOURCE_DIR}/gtsam/utils/*.py")
foreach(util_file ${GTSAM_PYTHON_UTIL_FILES})
configure_file(${util_file} "${GTSAM_MODULE_PATH}/utils/${test_file}" COPYONLY)

2
python/README.md
View File

@ -13,7 +13,7 @@ For instructions on updating the version of the [wrap library](https://github.co
use the `-DGTSAM_PYTHON_VERSION=3.6` option when running `cmake` otherwise the default interpreter will be used.
- If the interpreter is inside an environment (such as an anaconda environment or virtualenv environment),
then the environment should be active while building GTSAM.
- This wrapper needs `pyparsing(>=2.4.2)`, and `numpy(>=1.11.0)`. These can be installed as follows:
- This wrapper needs [pyparsing(>=2.4.2)](https://github.com/pyparsing/pyparsing), [pybind-stubgen>=2.5.1](https://github.com/sizmailov/pybind11-stubgen) and [numpy(>=1.11.0)](https://numpy.org/). These can all be installed as follows:
```bash
pip install -r <gtsam_folder>/python/dev_requirements.txt

120
python/gtsam/examples/EssentialViewGraphExample.py Normal file
View File

@ -0,0 +1,120 @@
"""
GTSAM Copyright 2010, Georgia Tech Research Corporation,
Atlanta, Georgia 30332-0415
All Rights Reserved
Authors: Frank Dellaert, et al. (see THANKS for the full author list)
See LICENSE for the license information
"""
"""
Python version of EssentialViewGraphExample.cpp
View-graph calibration with essential matrices.
Author: Frank Dellaert
Date: October 2024
"""
import numpy as np
from gtsam.examples import SFMdata
import gtsam
from gtsam import Cal3f, EdgeKey, EssentialMatrix
from gtsam import EssentialTransferFactorCal3f as Factor
from gtsam import (LevenbergMarquardtOptimizer, LevenbergMarquardtParams,
NonlinearFactorGraph, PinholeCameraCal3f, Values)
# For symbol shorthand (e.g., X(0), L(1))
K = gtsam.symbol_shorthand.K
# Formatter function for printing keys
def formatter(key):
sym = gtsam.Symbol(key)
if sym.chr() == ord("k"):
return f"k{sym.index()}"
else:
edge = EdgeKey(key)
return f"({edge.i()},{edge.j()})"
def main():
# Define the camera calibration parameters
cal = Cal3f(50.0, 50.0, 50.0)
# Create the set of 8 ground-truth landmarks
points = SFMdata.createPoints()
# Create the set of 4 ground-truth poses
poses = SFMdata.posesOnCircle(4, 30)
# Calculate ground truth essential matrices, 1 and 2 poses apart
E1 = EssentialMatrix.FromPose3(poses[0].between(poses[1]))
E2 = EssentialMatrix.FromPose3(poses[0].between(poses[2]))
# Simulate measurements from each camera pose
p = [[None for _ in range(8)] for _ in range(4)]
for i in range(4):
camera = PinholeCameraCal3f(poses[i], cal)
for j in range(8):
p[i][j] = camera.project(points[j])
# Create the factor graph
graph = NonlinearFactorGraph()
for a in range(4):
b = (a + 1) % 4 # Next camera
c = (a + 2) % 4 # Camera after next
# Collect data for the three factors
tuples1 = []
tuples2 = []
tuples3 = []
for j in range(8):
tuples1.append((p[a][j], p[b][j], p[c][j]))
tuples2.append((p[a][j], p[c][j], p[b][j]))
tuples3.append((p[c][j], p[b][j], p[a][j]))
# Add transfer factors between views a, b, and c.
graph.add(Factor(EdgeKey(a, c), EdgeKey(b, c), tuples1))
graph.add(Factor(EdgeKey(a, b), EdgeKey(b, c), tuples2))
graph.add(Factor(EdgeKey(a, c), EdgeKey(a, b), tuples3))
graph.print("graph", formatter)
# Create a delta vector to perturb the ground truth (small perturbation)
delta = np.ones(5) * 1e-2
# Create the initial estimate for essential matrices
initialEstimate = Values()
for a in range(4):
b = (a + 1) % 4 # Next camera
c = (a + 2) % 4 # Camera after next
initialEstimate.insert(EdgeKey(a, b).key(), E1.retract(delta))
initialEstimate.insert(EdgeKey(a, c).key(), E2.retract(delta))
# Insert initial calibrations
for i in range(4):
initialEstimate.insert(K(i), cal)
# Optimize the graph and print results
params = LevenbergMarquardtParams()
params.setlambdaInitial(1000.0) # Initialize lambda to a high value
params.setVerbosityLM("SUMMARY")
optimizer = LevenbergMarquardtOptimizer(graph, initialEstimate, params)
result = optimizer.optimize()
print("Initial error = ", graph.error(initialEstimate))
print("Final error = ", graph.error(result))
# Print final results
print("Final Results:")
result.print("", formatter)
# Print ground truth essential matrices
print("Ground Truth E1:\n", E1)
print("Ground Truth E2:\n", E2)
if __name__ == "__main__":
main()

41
python/gtsam/examples/SFMExample.py
View File

@ -9,20 +9,22 @@ See LICENSE for the license information
A structure-from-motion problem on a simulated dataset
"""
import gtsam
import matplotlib.pyplot as plt
import numpy as np
import gtsam
from gtsam import symbol_shorthand
L = symbol_shorthand.L
X = symbol_shorthand.X
from gtsam.examples import SFMdata
from gtsam import (Cal3_S2, DoglegOptimizer,
GenericProjectionFactorCal3_S2, Marginals,
NonlinearFactorGraph, PinholeCameraCal3_S2, Point3,
Pose3, PriorFactorPoint3, PriorFactorPose3, Rot3, Values)
from gtsam.utils import plot
from gtsam import (Cal3_S2, DoglegOptimizer, GenericProjectionFactorCal3_S2,
Marginals, NonlinearFactorGraph, PinholeCameraCal3_S2,
PriorFactorPoint3, PriorFactorPose3, Values)
def main():
"""
@ -43,7 +45,7 @@ def main():
Finally, once all of the factors have been added to our factor graph, we will want to
solve/optimize to graph to find the best (Maximum A Posteriori) set of variable values.
GTSAM includes several nonlinear optimizers to perform this step. Here we will use a
trust-region method known as Powell's Degleg
trust-region method known as Powell's Dogleg
The nonlinear solvers within GTSAM are iterative solvers, meaning they linearize the
nonlinear functions around an initial linearization point, then solve the linear system
@ -62,7 +64,7 @@ def main():
points = SFMdata.createPoints()
# Create the set of ground-truth poses
poses = SFMdata.createPoses(K)
poses = SFMdata.createPoses()
# Create a factor graph
graph = NonlinearFactorGraph()
@ -78,8 +80,7 @@ def main():
camera = PinholeCameraCal3_S2(pose, K)
for j, point in enumerate(points):
measurement = camera.project(point)
factor = GenericProjectionFactorCal3_S2(
measurement, measurement_noise, X(i), L(j), K)
factor = GenericProjectionFactorCal3_S2(measurement, measurement_noise, X(i), L(j), K)
graph.push_back(factor)
# Because the structure-from-motion problem has a scale ambiguity, the problem is still under-constrained
@ -88,28 +89,29 @@ def main():
point_noise = gtsam.noiseModel.Isotropic.Sigma(3, 0.1)
factor = PriorFactorPoint3(L(0), points[0], point_noise)
graph.push_back(factor)
graph.print('Factor Graph:\n')
graph.print("Factor Graph:\n")
# Create the data structure to hold the initial estimate to the solution
# Intentionally initialize the variables off from the ground truth
initial_estimate = Values()
rng = np.random.default_rng()
for i, pose in enumerate(poses):
transformed_pose = pose.retract(0.1*np.random.randn(6,1))
transformed_pose = pose.retract(0.1 * rng.standard_normal(6).reshape(6, 1))
initial_estimate.insert(X(i), transformed_pose)
for j, point in enumerate(points):
transformed_point = point + 0.1*np.random.randn(3)
transformed_point = point + 0.1 * rng.standard_normal(3)
initial_estimate.insert(L(j), transformed_point)
initial_estimate.print('Initial Estimates:\n')
initial_estimate.print("Initial Estimates:\n")
# Optimize the graph and print results
params = gtsam.DoglegParams()
params.setVerbosity('TERMINATION')
params.setVerbosity("TERMINATION")
optimizer = DoglegOptimizer(graph, initial_estimate, params)
print('Optimizing:')
print("Optimizing:")
result = optimizer.optimize()
result.print('Final results:\n')
print('initial error = {}'.format(graph.error(initial_estimate)))
print('final error = {}'.format(graph.error(result)))
result.print("Final results:\n")
print("initial error = {}".format(graph.error(initial_estimate)))
print("final error = {}".format(graph.error(result)))
marginals = Marginals(graph, result)
plot.plot_3d_points(1, result, marginals=marginals)
@ -117,5 +119,6 @@ def main():
plot.set_axes_equal(1)
plt.show()
if __name__ == '__main__':
if __name__ == "__main__":
main()

61
python/gtsam/examples/SFMdata.py
View File

@ -3,14 +3,14 @@ A structure-from-motion example with landmarks
- The landmarks form a 10 meter cube
- The robot rotates around the landmarks, always facing towards the cube
"""
# pylint: disable=invalid-name, E1101
from typing import List
import numpy as np
import gtsam
from gtsam import Cal3_S2, Point3, Pose3
from gtsam import Point3, Pose3, Rot3
def createPoints() -> List[Point3]:
@ -28,16 +28,49 @@ def createPoints() -> List[Point3]:
return points
def createPoses(K: Cal3_S2) -> List[Pose3]:
"""Generate a set of ground-truth camera poses arranged in a circle about the origin."""
radius = 40.0
height = 10.0
angles = np.linspace(0, 2 * np.pi, 8, endpoint=False)
up = gtsam.Point3(0, 0, 1)
target = gtsam.Point3(0, 0, 0)
poses = []
for theta in angles:
position = gtsam.Point3(radius * np.cos(theta), radius * np.sin(theta), height)
camera = gtsam.PinholeCameraCal3_S2.Lookat(position, target, up, K)
poses.append(camera.pose())
_M_PI_2 = np.pi / 2
_M_PI_4 = np.pi / 4
def createPoses(
init: Pose3 = Pose3(Rot3.Ypr(_M_PI_2, 0, -_M_PI_2), Point3(30, 0, 0)),
delta: Pose3 = Pose3(
Rot3.Ypr(0, -_M_PI_4, 0),
Point3(np.sin(_M_PI_4) * 30, 0, 30 * (1 - np.sin(_M_PI_4))),
),
steps: int = 8,
) -> List[Pose3]:
"""
Create a set of ground-truth poses
Default values give a circular trajectory, radius 30 at pi/4 intervals,
always facing the circle center
"""
poses = [init]
for _ in range(1, steps):
poses.append(poses[-1].compose(delta))
return poses
def posesOnCircle(num_cameras=8, R=30):
"""Create regularly spaced poses with specified radius and number of cameras."""
theta = 2 * np.pi / num_cameras
# Initial pose at angle 0, position (R, 0, 0), facing the center with Y-axis pointing down
init_rotation = Rot3.Ypr(_M_PI_2, 0, -_M_PI_2)
init_position = np.array([R, 0, 0])
init = Pose3(init_rotation, init_position)
# Delta rotation: rotate by -theta around Z-axis (counterclockwise movement)
delta_rotation = Rot3.Ypr(0, -theta, 0)
# Delta translation in world frame
delta_translation_world = np.array([R * (np.cos(theta) - 1), R * np.sin(theta), 0])
# Transform delta translation to local frame of the camera
delta_translation_local = init.rotation().unrotate(delta_translation_world)
# Define delta pose
delta = Pose3(delta_rotation, delta_translation_local)
# Generate poses
return createPoses(init, delta, num_cameras)

3
python/gtsam/examples/TranslationAveragingExample.py
View File

@ -31,8 +31,7 @@ def get_data() -> Tuple[gtsam.Values, List[gtsam.BinaryMeasurementUnit3]]:
that lie on a circle and face the center. The poses of 8 cameras are obtained from SFMdata
and the unit translations directions between some camera pairs are computed from their
global translations. """
fx, fy, s, u0, v0 = 50.0, 50.0, 0.0, 50.0, 50.0
wTc_list = SFMdata.createPoses(gtsam.Cal3_S2(fx, fy, s, u0, v0))
wTc_list = SFMdata.createPoses()
# Rotations of the cameras in the world frame.
wRc_values = gtsam.Values()
# Normalized translation directions from camera i to camera j

403
python/gtsam/examples/ViewGraphComparison.py Normal file
View File

@ -0,0 +1,403 @@
"""
Compare several methods for optimizing the view-graph.
We measure the distance from the ground truth in terms of the norm of
local coordinates (geodesic distance) on the F-manifold.
We also plot the final error of the optimization.
Author: Frank Dellaert (with heavy assist from ChatGPT)
Date: October 2024
"""
import argparse
import matplotlib.pyplot as plt
import numpy as np
from gtsam.examples import SFMdata
import gtsam
from gtsam import (
Cal3f,
EdgeKey,
EssentialMatrix,
FundamentalMatrix,
LevenbergMarquardtOptimizer,
LevenbergMarquardtParams,
NonlinearFactorGraph,
PinholeCameraCal3f,
SimpleFundamentalMatrix,
Values,
)
# For symbol shorthand (e.g., K(0), K(1))
K = gtsam.symbol_shorthand.K
# Methods to compare
methods = ["SimpleF", "Fundamental", "Essential+Ks", "Essential+K", "Calibrated", "Binary+Ks", "Binary+K"]
# Formatter function for printing keys
def formatter(key):
sym = gtsam.Symbol(key)
if sym.chr() == ord("k"):
return f"k{sym.index()}"
else:
edge = EdgeKey(key)
return f"({edge.i()},{edge.j()})"
def simulate_geometry(num_cameras, rng, num_random_points=12):
"""simulate geometry (points and poses)"""
# Define the camera calibration parameters
cal = Cal3f(50.0, 50.0, 50.0)
# Create the set of 8 ground-truth landmarks
points = SFMdata.createPoints()
# Create extra random points in the -10,10 cube around the origin
extra_points = rng.uniform(-10, 10, (num_random_points, 3))
points.extend([gtsam.Point3(p) for p in extra_points])
# Create the set of ground-truth poses
poses = SFMdata.posesOnCircle(num_cameras, 30)
return points, poses, cal
def simulate_data(points, poses, cal, rng, noise_std):
"""Simulate measurements from each camera pose"""
measurements = [[None for _ in points] for _ in poses]
for i, pose in enumerate(poses):
camera = PinholeCameraCal3f(pose, cal)
for j, point in enumerate(points):
projection = camera.project(point)
noise = rng.normal(0, noise_std, size=2)
measurements[i][j] = projection + noise
return measurements
def compute_ground_truth(method, poses, cal):
"""Function to compute ground truth edge variables."""
E1 = EssentialMatrix.FromPose3(poses[0].between(poses[1]))
E2 = EssentialMatrix.FromPose3(poses[0].between(poses[2]))
F1 = FundamentalMatrix(cal.K(), E1, cal.K())
F2 = FundamentalMatrix(cal.K(), E2, cal.K())
if method == "Fundamental":
return F1, F2
elif method == "SimpleF":
f = cal.fx()
c = cal.principalPoint()
SF1 = SimpleFundamentalMatrix(E1, f, f, c, c)
SF2 = SimpleFundamentalMatrix(E2, f, f, c, c)
return SF1, SF2
else:
return E1, E2
def build_factor_graph(method, num_cameras, measurements, cal):
"""build the factor graph"""
graph = NonlinearFactorGraph()
# Determine the FactorClass based on the method
if method == "Fundamental":
FactorClass = gtsam.TransferFactorFundamentalMatrix
elif method == "SimpleF":
FactorClass = gtsam.TransferFactorSimpleFundamentalMatrix
elif method in ["Essential+Ks", "Essential+K"]:
FactorClass = gtsam.EssentialTransferFactorKCal3f
elif method == "Binary+K":
FactorClass = gtsam.EssentialMatrixFactor4Cal3f
elif method == "Binary+Ks":
FactorClass = gtsam.EssentialMatrixFactor5Cal3f
elif method == "Calibrated":
FactorClass = gtsam.EssentialTransferFactorCal3f
else:
raise ValueError(f"Unknown method {method}")
# Add priors on calibrations if necessary
if method in ["Essential+Ks", "Binary+Ks"]:
for i in range(num_cameras):
model = gtsam.noiseModel.Isotropic.Sigma(1, 1000.0)
graph.addPriorCal3f(K(i), cal, model)
elif method in ["Essential+K", "Binary+K"]:
model = gtsam.noiseModel.Isotropic.Sigma(1, 1000.0)
graph.addPriorCal3f(K(0), cal, model)
z = measurements # shorthand
for a in range(num_cameras):
b = (a + 1) % num_cameras # Next camera
c = (a + 2) % num_cameras # Camera after next
if method in ["Binary+Ks", "Binary+K"]:
# Add binary Essential Matrix factors
ab, ac = EdgeKey(a, b).key(), EdgeKey(a, c).key()
for j in range(len(measurements[0])):
if method == "Binary+Ks":
graph.add(FactorClass(ab, K(a), K(b), z[a][j], z[b][j]))
graph.add(FactorClass(ac, K(a), K(c), z[a][j], z[c][j]))
else: # Binary+K
graph.add(FactorClass(ab, K(0), z[a][j], z[b][j]))
graph.add(FactorClass(ac, K(0), z[a][j], z[c][j]))
else:
# Add transfer factors between views a, b, and c
# Vectors to collect tuples for each factor
tuples1 = []
tuples2 = []
tuples3 = []
for j in range(len(measurements[0])):
tuples1.append((z[a][j], z[b][j], z[c][j]))
tuples2.append((z[a][j], z[c][j], z[b][j]))
tuples3.append((z[c][j], z[b][j], z[a][j]))
# Add transfer factors between views a, b, and c.
if method in ["Calibrated"]:
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(b, c), tuples1, cal))
graph.add(FactorClass(EdgeKey(a, b), EdgeKey(b, c), tuples2, cal))
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(a, b), tuples3, cal))
elif method == "Essential+K":
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(b, c), K(0), tuples1))
graph.add(FactorClass(EdgeKey(a, b), EdgeKey(b, c), K(0), tuples2))
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(a, b), K(0), tuples3))
else:
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(b, c), tuples1))
graph.add(FactorClass(EdgeKey(a, b), EdgeKey(b, c), tuples2))
graph.add(FactorClass(EdgeKey(a, c), EdgeKey(a, b), tuples3))
return graph
def get_initial_estimate(method, num_cameras, ground_truth, cal):
"""get initial estimate for method"""
initialEstimate = Values()
total_dimension = 0
if method in ["Fundamental", "SimpleF"]:
F1, F2 = ground_truth
for a in range(num_cameras):
b = (a + 1) % num_cameras # Next camera
c = (a + 2) % num_cameras # Camera after next
initialEstimate.insert(EdgeKey(a, b).key(), F1)
initialEstimate.insert(EdgeKey(a, c).key(), F2)
total_dimension += F1.dim() + F2.dim()
elif method in ["Essential+Ks", "Essential+K", "Binary+Ks", "Binary+K", "Calibrated"]:
E1, E2 = ground_truth
for a in range(num_cameras):
b = (a + 1) % num_cameras
c = (a + 2) % num_cameras
# initialEstimate.insert(EdgeKey(a, b).key(), E1.retract(0.1 * np.ones((5, 1))))
# initialEstimate.insert(EdgeKey(a, c).key(), E2.retract(0.1 * np.ones((5, 1))))
initialEstimate.insert(EdgeKey(a, b).key(), E1)
initialEstimate.insert(EdgeKey(a, c).key(), E2)
total_dimension += E1.dim() + E2.dim()
# Insert initial calibrations
if method in ["Essential+Ks", "Binary+Ks"]:
for i in range(num_cameras):
initialEstimate.insert(K(i), cal)
total_dimension += cal.dim()
elif method in ["Essential+K", "Binary+K"]:
initialEstimate.insert(K(0), cal)
total_dimension += cal.dim()
print(f"Total dimension of the problem: {total_dimension}")
return initialEstimate
def optimize(graph, initialEstimate, method):
"""optimize the graph"""
params = LevenbergMarquardtParams()
if method not in ["Calibrated", "Binary+K", "Binary+Ks"]:
params.setlambdaInitial(1e10) # Initialize lambda to a high value
params.setlambdaUpperBound(1e10)
# params.setAbsoluteErrorTol(0.1)
params.setVerbosityLM("SUMMARY")
optimizer = LevenbergMarquardtOptimizer(graph, initialEstimate, params)
result = optimizer.optimize()
iterations = optimizer.iterations()
return result, iterations
def compute_distances(method, result, ground_truth, num_cameras, cal):
"""Compute geodesic distances from ground truth"""
distances = []
F1, F2 = ground_truth["Fundamental"]
for a in range(num_cameras):
b = (a + 1) % num_cameras
c = (a + 2) % num_cameras
key_ab = EdgeKey(a, b).key()
key_ac = EdgeKey(a, c).key()
if method in ["Essential+Ks", "Essential+K", "Binary+Ks", "Binary+K", "Calibrated"]:
E_est_ab = result.atEssentialMatrix(key_ab)
E_est_ac = result.atEssentialMatrix(key_ac)
# Compute estimated FundamentalMatrices
if method == "Fundamental":
F_est_ab = result.atFundamentalMatrix(key_ab)
F_est_ac = result.atFundamentalMatrix(key_ac)
elif method == "SimpleF":
SF_est_ab = result.atSimpleFundamentalMatrix(key_ab).matrix()
SF_est_ac = result.atSimpleFundamentalMatrix(key_ac).matrix()
F_est_ab = FundamentalMatrix(SF_est_ab)
F_est_ac = FundamentalMatrix(SF_est_ac)
elif method in ["Essential+Ks", "Binary+Ks"]:
# Retrieve calibrations from result for each camera
cal_a = result.atCal3f(K(a))
cal_b = result.atCal3f(K(b))
cal_c = result.atCal3f(K(c))
F_est_ab = FundamentalMatrix(cal_a.K(), E_est_ab, cal_b.K())
F_est_ac = FundamentalMatrix(cal_a.K(), E_est_ac, cal_c.K())
elif method in ["Essential+K", "Binary+K"]:
# Use single shared calibration
cal_shared = result.atCal3f(K(0))
F_est_ab = FundamentalMatrix(cal_shared.K(), E_est_ab, cal_shared.K())
F_est_ac = FundamentalMatrix(cal_shared.K(), E_est_ac, cal_shared.K())
elif method == "Calibrated":
# Use ground truth calibration
F_est_ab = FundamentalMatrix(cal.K(), E_est_ab, cal.K())
F_est_ac = FundamentalMatrix(cal.K(), E_est_ac, cal.K())
else:
raise ValueError(f"Unknown method {method}")
# Compute local coordinates (geodesic distance on the F-manifold)
dist_ab = np.linalg.norm(F1.localCoordinates(F_est_ab))
dist_ac = np.linalg.norm(F2.localCoordinates(F_est_ac))
distances.append(dist_ab)
distances.append(dist_ac)
return distances
def plot_results(results):
"""plot results"""
methods = list(results.keys())
final_errors = [results[method]["final_error"] for method in methods]
distances = [results[method]["distances"] for method in methods]
iterations = [results[method]["iterations"] for method in methods]
fig, ax1 = plt.subplots()
color = "tab:red"
ax1.set_xlabel("Method")
ax1.set_ylabel("Median Error (log scale)", color=color)
ax1.set_yscale("log")
ax1.bar(methods, final_errors, color=color, alpha=0.6)
ax1.tick_params(axis="y", labelcolor=color)
ax2 = ax1.twinx()
color = "tab:blue"
ax2.set_ylabel("Median Geodesic Distance", color=color)
ax2.plot(methods, distances, color=color, marker="o", linestyle="-")
ax2.tick_params(axis="y", labelcolor=color)
# Annotate the blue data points with the average number of iterations
for i, method in enumerate(methods):
ax2.annotate(
f"{iterations[i]:.1f}",
(i, distances[i]),
textcoords="offset points",
xytext=(0, 10),
ha="center",
color=color,
)
plt.title("Comparison of Methods (Labels show avg iterations)")
fig.tight_layout()
plt.show()
# Main function
def main():
# Parse command line arguments
parser = argparse.ArgumentParser(description="Compare Fundamental and Essential Matrix Methods")
parser.add_argument("--num_cameras", type=int, default=4, help="Number of cameras (default: 4)")
parser.add_argument("--num_extra_points", type=int, default=12, help="Number of extra random points (default: 12)")
parser.add_argument("--num_trials", type=int, default=5, help="Number of trials (default: 5)")
parser.add_argument("--seed", type=int, default=42, help="Random seed (default: 42)")
parser.add_argument("--noise_std", type=float, default=0.5, help="Standard deviation of noise (default: 0.5)")
args = parser.parse_args()
# Initialize the random number generator
rng = np.random.default_rng(seed=args.seed)
# Initialize results dictionary
results = {method: {"distances": [], "final_error": [], "iterations": []} for method in methods}
# Simulate geometry
points, poses, cal = simulate_geometry(args.num_cameras, rng, args.num_extra_points)
# Compute ground truth matrices
ground_truth = {method: compute_ground_truth(method, poses, cal) for method in methods}
# Get initial estimates
initial_estimate: dict[Values] = {
method: get_initial_estimate(method, args.num_cameras, ground_truth[method], cal) for method in methods
}
simple_f_result: Values = Values()
for trial in range(args.num_trials):
print(f"\nTrial {trial + 1}/{args.num_trials}")
# Simulate data
measurements = simulate_data(points, poses, cal, rng, args.noise_std)
for method in methods:
print(f"\nRunning method: {method}")
# Build the factor graph
graph = build_factor_graph(method, args.num_cameras, measurements, cal)
# For F, initialize from SimpleF:
if method == "Fundamental":
initial_estimate[method] = simple_f_result
# Optimize the graph
result, iterations = optimize(graph, initial_estimate[method], method)
# Store SimpleF result as a set of FundamentalMatrices
if method == "SimpleF":
simple_f_result = Values()
for a in range(args.num_cameras):
b = (a + 1) % args.num_cameras # Next camera
c = (a + 2) % args.num_cameras # Camera after next
key_ab = EdgeKey(a, b).key()
key_ac = EdgeKey(a, c).key()
F1 = result.atSimpleFundamentalMatrix(key_ab).matrix()
F2 = result.atSimpleFundamentalMatrix(key_ac).matrix()
simple_f_result.insert(key_ab, FundamentalMatrix(F1))
simple_f_result.insert(key_ac, FundamentalMatrix(F2))
# Compute distances from ground truth
distances = compute_distances(method, result, ground_truth, args.num_cameras, cal)
# Compute final error
final_error = graph.error(result)
if method in ["Binary+K", "Binary+Ks"]:
final_error *= cal.f() * cal.f()
# Store results
results[method]["distances"].extend(distances)
results[method]["final_error"].append(final_error)
results[method]["iterations"].append(iterations)
print(f"Method: {method}")
print(f"Final Error: {final_error:.3f}")
print(f"Mean Geodesic Distance: {np.mean(distances):.3f}")
print(f"Number of Iterations: {iterations}\n")
# Average results over trials
for method in methods:
results[method]["final_error"] = np.median(results[method]["final_error"])
results[method]["distances"] = np.median(results[method]["distances"])
results[method]["iterations"] = np.median(results[method]["iterations"])
# Plot results
plot_results(results)
if __name__ == "__main__":
main()

111
python/gtsam/examples/ViewGraphExample.py Normal file
View File

@ -0,0 +1,111 @@
"""
GTSAM Copyright 2010, Georgia Tech Research Corporation,
Atlanta, Georgia 30332-0415
All Rights Reserved
Authors: Frank Dellaert, et al. (see THANKS for the full author list)
See LICENSE for the license information
"""
"""
Python version of ViewGraphExample.cpp
View-graph calibration on a simulated dataset, a la Sweeney 2015
Author: Frank Dellaert
Date: October 2024
"""
import numpy as np
from gtsam.examples import SFMdata
from gtsam import (Cal3_S2, EdgeKey, FundamentalMatrix,
LevenbergMarquardtOptimizer, LevenbergMarquardtParams,
NonlinearFactorGraph, PinholeCameraCal3_S2)
from gtsam import TransferFactorFundamentalMatrix as Factor
from gtsam import Values
# Formatter function for printing keys
def formatter(key):
edge = EdgeKey(key)
return f"({edge.i()},{edge.j()})"
def main():
# Define the camera calibration parameters
cal = Cal3_S2(50.0, 50.0, 0.0, 50.0, 50.0)
# Create the set of 8 ground-truth landmarks
points = SFMdata.createPoints()
# Create the set of 4 ground-truth poses
poses = SFMdata.posesOnCircle(4, 30)
# Calculate ground truth fundamental matrices, 1 and 2 poses apart
F1 = FundamentalMatrix(cal.K(), poses[0].between(poses[1]), cal.K())
F2 = FundamentalMatrix(cal.K(), poses[0].between(poses[2]), cal.K())
# Simulate measurements from each camera pose
p = [[None for _ in range(8)] for _ in range(4)]
for i in range(4):
camera = PinholeCameraCal3_S2(poses[i], cal)
for j in range(8):
p[i][j] = camera.project(points[j])
# Create the factor graph
graph = NonlinearFactorGraph()
for a in range(4):
b = (a + 1) % 4 # Next camera
c = (a + 2) % 4 # Camera after next
# Vectors to collect tuples for each factor
tuples1 = []
tuples2 = []
tuples3 = []
# Collect data for the three factors
for j in range(8):
tuples1.append((p[a][j], p[b][j], p[c][j]))
tuples2.append((p[a][j], p[c][j], p[b][j]))
tuples3.append((p[c][j], p[b][j], p[a][j]))
# Add transfer factors between views a, b, and c.
graph.add(Factor(EdgeKey(a, c), EdgeKey(b, c), tuples1))
graph.add(Factor(EdgeKey(a, b), EdgeKey(b, c), tuples2))
graph.add(Factor(EdgeKey(a, c), EdgeKey(a, b), tuples3))
# Print the factor graph
graph.print("Factor Graph:\n", formatter)
# Create a delta vector to perturb the ground truth
delta = np.array([1, 2, 3, 4, 5, 6, 7]) * 1e-5
# Create the data structure to hold the initial estimate to the solution
initialEstimate = Values()
for a in range(4):
b = (a + 1) % 4 # Next camera
c = (a + 2) % 4 # Camera after next
initialEstimate.insert(EdgeKey(a, b).key(), F1.retract(delta))
initialEstimate.insert(EdgeKey(a, c).key(), F2.retract(delta))
initialEstimate.print("Initial Estimates:\n", formatter)
graph.printErrors(initialEstimate, "Initial Errors:\n", formatter)
# Optimize the graph and print results
params = LevenbergMarquardtParams()
params.setlambdaInitial(1000.0) # Initialize lambda to a high value
params.setVerbosityLM("SUMMARY")
optimizer = LevenbergMarquardtOptimizer(graph, initialEstimate, params)
result = optimizer.optimize()
print(f"Initial error = {graph.error(initialEstimate)}")
print(f"Final error = {graph.error(result)}")
result.print("Final Results:\n", formatter)
print("Ground Truth F1:\n", F1.matrix())
print("Ground Truth F2:\n", F2.matrix())
if __name__ == "__main__":
main()

2
python/gtsam/examples/VisualISAM2Example.py
View File

@ -73,7 +73,7 @@ def visual_ISAM2_example():
points = SFMdata.createPoints()
# Create the set of ground-truth poses
poses = SFMdata.createPoses(K)
poses = SFMdata.createPoses()
# Create an iSAM2 object. Unlike iSAM1, which performs periodic batch steps
# to maintain proper linearization and efficient variable ordering, iSAM2

2
python/gtsam/examples/VisualISAMExample.py
View File

@ -36,7 +36,7 @@ def main():
# Create the set of ground-truth landmarks
points = SFMdata.createPoints()
# Create the set of ground-truth poses
poses = SFMdata.createPoses(K)
poses = SFMdata.createPoses()
# Create a NonlinearISAM object which will relinearize and reorder the variables
# every "reorderInterval" updates

285
python/gtsam/tests/test_FundamentalMatrix.py Normal file
View File

@ -0,0 +1,285 @@
"""
GTSAM Copyright 2010-2019, Georgia Tech Research Corporation,
Atlanta, Georgia 30332-0415
All Rights Reserved
See LICENSE for the license information
FundamentalMatrix unit tests.
Author: Frank Dellaert
"""
# pylint: disable=no-name-in-module
import unittest
import numpy as np
from gtsam.examples import SFMdata
from numpy.testing import assert_almost_equal
import gtsam
from gtsam import (Cal3_S2, EssentialMatrix, FundamentalMatrix,
PinholeCameraCal3_S2, Point2, Point3, Rot3,
SimpleFundamentalMatrix, Unit3)
class TestFundamentalMatrix(unittest.TestCase):
def setUp(self):
# Create two rotations and corresponding fundamental matrix F
self.trueU = Rot3.Yaw(np.pi / 2)
self.trueV = Rot3.Yaw(np.pi / 4)
self.trueS = 0.5
self.trueF = FundamentalMatrix(self.trueU.matrix(), self.trueS, self.trueV.matrix())
def test_localCoordinates(self):
expected = np.zeros(7) # Assuming 7 dimensions for U, V, and s
actual = self.trueF.localCoordinates(self.trueF)
assert_almost_equal(expected, actual, decimal=8)
def test_retract(self):
actual = self.trueF.retract(np.zeros(7))
self.assertTrue(self.trueF.equals(actual, 1e-9))
def test_RoundTrip(self):
d = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7])
hx = self.trueF.retract(d)
actual = self.trueF.localCoordinates(hx)
assert_almost_equal(d, actual, decimal=8)
class TestSimpleStereo(unittest.TestCase):
def setUp(self):
# Create the simplest SimpleFundamentalMatrix, a stereo pair
self.defaultE = EssentialMatrix(Rot3(), Unit3(1, 0, 0))
self.zero = Point2(0.0, 0.0)
self.stereoF = SimpleFundamentalMatrix(self.defaultE, 1.0, 1.0, self.zero, self.zero)
def test_Conversion(self):
convertedF = FundamentalMatrix(self.stereoF.matrix())
assert_almost_equal(self.stereoF.matrix(), convertedF.matrix(), decimal=8)
def test_localCoordinates(self):
expected = np.zeros(7)
actual = self.stereoF.localCoordinates(self.stereoF)
assert_almost_equal(expected, actual, decimal=8)
def test_retract(self):
actual = self.stereoF.retract(np.zeros(9))
self.assertTrue(self.stereoF.equals(actual, 1e-9))
def test_RoundTrip(self):
d = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7])
hx = self.stereoF.retract(d)
actual = self.stereoF.localCoordinates(hx)
assert_almost_equal(d, actual, decimal=8)
def test_EpipolarLine(self):
# Create a point in b
p_b = np.array([0, 2, 1])
# Convert the point to a horizontal line in a
l_a = self.stereoF.matrix() @ p_b
# Check if the line is horizontal at height 2
expected = np.array([0, -1, 2])
assert_almost_equal(l_a, expected, decimal=8)
class TestPixelStereo(unittest.TestCase):
def setUp(self):
# Create a stereo pair in pixels, zero principal points
self.focalLength = 1000.0
self.defaultE = EssentialMatrix(Rot3(), Unit3(1, 0, 0))
self.zero = Point2(0.0, 0.0)
self.pixelStereo = SimpleFundamentalMatrix(
self.defaultE, self.focalLength, self.focalLength, self.zero, self.zero
)
def test_Conversion(self):
expected = self.pixelStereo.matrix()
convertedF = FundamentalMatrix(self.pixelStereo.matrix())
# Check equality of F-matrices up to a scale
actual = convertedF.matrix()
scale = expected[1, 2] / actual[1, 2]
actual *= scale
assert_almost_equal(expected, actual, decimal=5)
def test_PointInBToHorizontalLineInA(self):
# Create a point in b
p_b = np.array([0, 300, 1])
# Convert the point to a horizontal line in a
l_a = self.pixelStereo.matrix() @ p_b
# Check if the line is horizontal at height 0.3
expected = np.array([0, -0.001, 0.3])
assert_almost_equal(l_a, expected, decimal=8)
class TestRotatedPixelStereo(unittest.TestCase):
def setUp(self):
# Create a stereo pair with the right camera rotated 90 degrees
self.focalLength = 1000.0
self.zero = Point2(0.0, 0.0)
self.aRb = Rot3.Rz(np.pi / 2) # Rotate 90 degrees around the Z-axis
self.rotatedE = EssentialMatrix(self.aRb, Unit3(1, 0, 0))
self.rotatedPixelStereo = SimpleFundamentalMatrix(
self.rotatedE, self.focalLength, self.focalLength, self.zero, self.zero
)
def test_Conversion(self):
expected = self.rotatedPixelStereo.matrix()
convertedF = FundamentalMatrix(self.rotatedPixelStereo.matrix())
# Check equality of F-matrices up to a scale
actual = convertedF.matrix()
scale = expected[1, 2] / actual[1, 2]
actual *= scale
assert_almost_equal(expected, actual, decimal=4)
def test_PointInBToHorizontalLineInA(self):
# Create a point in b
p_b = np.array([300, 0, 1])
# Convert the point to a horizontal line in a
l_a = self.rotatedPixelStereo.matrix() @ p_b
# Check if the line is horizontal at height 0.3
expected = np.array([0, -0.001, 0.3])
assert_almost_equal(l_a, expected, decimal=8)
class TestStereoWithPrincipalPoints(unittest.TestCase):
def setUp(self):
# Now check that principal points also survive conversion
self.focalLength = 1000.0
self.principalPoint = Point2(640 / 2, 480 / 2)
self.aRb = Rot3.Rz(np.pi / 2)
self.rotatedE = EssentialMatrix(self.aRb, Unit3(1, 0, 0))
self.stereoWithPrincipalPoints = SimpleFundamentalMatrix(
self.rotatedE, self.focalLength, self.focalLength, self.principalPoint, self.principalPoint
)
def test_Conversion(self):
expected = self.stereoWithPrincipalPoints.matrix()
convertedF = FundamentalMatrix(self.stereoWithPrincipalPoints.matrix())
# Check equality of F-matrices up to a scale
actual = convertedF.matrix()
scale = expected[1, 2] / actual[1, 2]
actual *= scale
assert_almost_equal(expected, actual, decimal=4)
class TestTripleF(unittest.TestCase):
def setUp(self):
# Generate three cameras on a circle, looking in
self.cameraPoses = SFMdata.posesOnCircle(3, 1.0)
self.focalLength = 1000.0
self.principalPoint = Point2(640 / 2, 480 / 2)
self.triplet = self.generateTripleF(self.cameraPoses)
def generateTripleF(self, cameraPoses):
F = []
for i in range(3):
j = (i + 1) % 3
iPj = cameraPoses[i].between(cameraPoses[j])
E = EssentialMatrix(iPj.rotation(), Unit3(iPj.translation()))
F_ij = SimpleFundamentalMatrix(
E, self.focalLength, self.focalLength, self.principalPoint, self.principalPoint
)
F.append(F_ij)
return {"Fab": F[0], "Fbc": F[1], "Fca": F[2]}
def transferToA(self, pb, pc):
return gtsam.EpipolarTransfer(self.triplet["Fab"].matrix(), pb, self.triplet["Fca"].matrix().transpose(), pc)
def transferToB(self, pa, pc):
return gtsam.EpipolarTransfer(self.triplet["Fab"].matrix().transpose(), pa, self.triplet["Fbc"].matrix(), pc)
def transferToC(self, pa, pb):
return gtsam.EpipolarTransfer(self.triplet["Fca"].matrix(), pa, self.triplet["Fbc"].matrix().transpose(), pb)
def test_Transfer(self):
triplet = self.triplet
# Check that they are all equal
self.assertTrue(triplet["Fab"].equals(triplet["Fbc"], 1e-9))
self.assertTrue(triplet["Fbc"].equals(triplet["Fca"], 1e-9))
self.assertTrue(triplet["Fca"].equals(triplet["Fab"], 1e-9))
# Now project a point into the three cameras
P = Point3(0.1, 0.2, 0.3)
K = Cal3_S2(self.focalLength, self.focalLength, 0.0, self.principalPoint[0], self.principalPoint[1])
p = []
for i in range(3):
# Project the point into each camera
camera = PinholeCameraCal3_S2(self.cameraPoses[i], K)
p_i = camera.project(P)
p.append(p_i)
# Check that transfer works
assert_almost_equal(p[0], self.transferToA(p[1], p[2]), decimal=9)
assert_almost_equal(p[1], self.transferToB(p[0], p[2]), decimal=9)
assert_almost_equal(p[2], self.transferToC(p[0], p[1]), decimal=9)
class TestManyCamerasCircle(unittest.TestCase):
N = 6
def setUp(self):
# Generate six cameras on a circle, looking in
self.cameraPoses = SFMdata.posesOnCircle(self.N, 1.0)
self.focalLength = 1000.0
self.principalPoint = Point2(640 / 2, 480 / 2)
self.manyFs = self.generateManyFs(self.cameraPoses)
def generateManyFs(self, cameraPoses):
F = []
for i in range(self.N):
j = (i + 1) % self.N
iPj = cameraPoses[i].between(cameraPoses[j])
E = EssentialMatrix(iPj.rotation(), Unit3(iPj.translation()))
F_ij = SimpleFundamentalMatrix(
E, self.focalLength, self.focalLength, self.principalPoint, self.principalPoint
)
F.append(F_ij)
return F
def test_Conversion(self):
for i in range(self.N):
expected = self.manyFs[i].matrix()
convertedF = FundamentalMatrix(self.manyFs[i].matrix())
# Check equality of F-matrices up to a scale
actual = convertedF.matrix()
scale = expected[1, 2] / actual[1, 2]
actual *= scale
# print(f"\n{np.round(expected, 3)}", f"\n{np.round(actual, 3)}")
assert_almost_equal(expected, actual, decimal=4)
def test_Transfer(self):
# Now project a point into the six cameras
P = Point3(0.1, 0.2, 0.3)
K = Cal3_S2(self.focalLength, self.focalLength, 0.0, self.principalPoint[0], self.principalPoint[1])
p = []
for i in range(self.N):
# Project the point into each camera
camera = PinholeCameraCal3_S2(self.cameraPoses[i], K)
p_i = camera.project(P)
p.append(p_i)
# Check that transfer works
for a in range(self.N):
b = (a + 1) % self.N
c = (a + 2) % self.N
# We transfer from a to b and from c to b,
# and check that the result lines up with the projected point in b.
transferred = gtsam.EpipolarTransfer(
self.manyFs[a].matrix().transpose(), # need to transpose for a->b
p[a],
self.manyFs[c].matrix(),
p[c],
)
assert_almost_equal(p[b], transferred, decimal=9)
if __name__ == "__main__":
unittest.main()